Olimpiade Sains Provinsi (OSP) 2015 - Fisika SMA
1.
Lihat 1 jawaban →Sebuah benda yg bergerak pada bidang 2 dimensi mendapat gaya konstan. Setelah detik pertama, kelajuan benda menjadi 1/3 dari kelajuan awal benda. Dan setelah detik selanjutnya (detik kedua), kelajuan benda menjadi 1/3 nya lagi (dibandingkan setelah detik pertama). Tunjukan apakah benda tersebut pernah mengalami berhenti sesaat selama proses pergerakannya? Jika pernah, tentukan kapan waktunya (t dalam sekon dan ambil acuan waktu t = 0 dari saat kelajuan benda masih V) !
2.
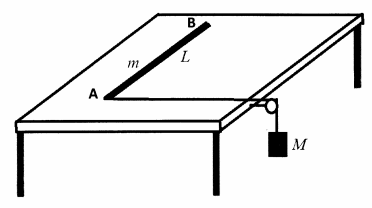
Lihat 2 jawaban →Sebuah batang tegar AB dengan paryang L bermassa m berada di atas meja horisontal licin. Sebuah tali tak bermassa dipasang pada katrol licin dimana ujung yang satu dihubungkan pada ujung batang A, sedangkan ujung tali satunya lagi dihubungkan dengan beban M (lihat gambar di bawah). Mula-mula batang AB tegak lurus dengan tali tersebut, kemudian beban M dilepaskan.
a. Pada saat beban M dilepaskan, tentukan tegangan tali, percepatan beban M serta percepatan pusat massa batang m.
b. Tentukan posisi titik pada batang (diukur dari A) yang memiliki percepatan nol pada saat beban M dtlepaskan.
3.
Jawab →Sebuah kereta bermassa M = 3 kg memiliki permukaan horisontal yang tersambung dengan permukaan berbentuk seperempat lingkaran berjari-jari R = 0,5 m (lihat gambar di bawah). Sebuah partikel bermassa m = 2 kg bergerak di atas permukaan horisontal kereta tersebut dengan kecepatan v = 15 m/s terhadap lantai. Pada saat partikel tersebut sudah bergerak di atas kereta, kereta tersebut berada dalam keadaan diam terhadap lantai. Seluruh permukaan bersifat licin dan tumbukan bersifat lenting sernpurna. Percepatan gravitasi g = 10 m/s2 ke bawah.
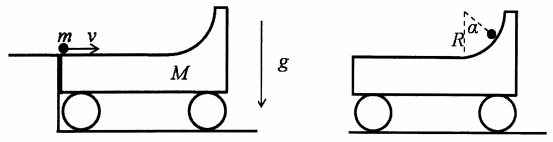
a. Pada saat partikel tersebut berada pada permukaan seperempat lingkaran dimana sudut yang dibentuk antara garis yang menghubungkan partikel dan pusat lingkaran dengan garis vertikal ke bawah adalah , tentukan masing-masing besar kecepatan partikel dan kecepatan kereta terhadap lantai sebagai fungsi
.
b. Tentukan kecepatan partikel terhadap lantar tepat ketika meninggalkan kereta.
c. Tentukan jarak yang ditempuh kereta sejak partikel meninggalkan kereta hingga kembali menumbuk kereta tersebut.
d. Ketika partikel tersebut kembali menumbuk kereta dan sudah berada pada lintasan horisontal kereta tersebut, tentukan besar kecepatan partikel dan kereta terhadap lantai.
4.
Lihat 1 jawaban →Sebuah satelit bergerak dalam orbit lingkaran di sekitar sebuah planet dengan periode revolusi sebesar T1 8 jam. Lintasan satelit tersebut akan diubah ke orbit lingkaran lainnya dengan periode sebesar T2 = 27 jam melalui cara sebagai berikut. Pertama, satelit tersebut pada orbit pertamanya seketika diubah besar kecepatannya tarrpa merubah arahnya, sehingga ia akan bergerak dalam orbit transisi yang berbentuk ellips. Ketika satelit tersebut telah menempuh jarak dari planet yang diinginkan, kecepatannya diubah seketika sesuai dengan orbit kedua dengan periode T2. Tentukan:
a. waktu yang dibutuhkan untuk berpindah dari orbit pertama ke orbit kedua.
b. prosentase perubahan besar kecepatan saterit pada keadaan pertama dan kedua relatif terhadap kecepatan masing-masing orbit lingkarannya.
5.
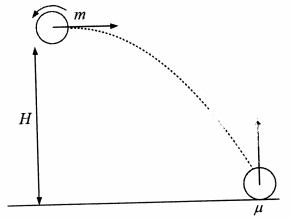
Lihat 1 jawaban →Sebuah bola ping-pong bermassa m = 3 gram dipukul sedemikian rupa sehingga bola tersebut memperoleh kecepatan horisontal pada ketinggian H = 20 cm di atas meja. Bola tersebut jugu berotasi terhadap sumbu horisontal yang tegak lurus pada kecepatan horisontal tersebut' Setelah menabrak meja dalam tumbukan yang bersifat elastik, bola tersebut terpental vertikai ke atas tanpa rotasi. Karena ketidakrataan permukaan meja, koefisien gesek kinetik antarabola dengan meja µ = 0,25. Asumsikan bahwa tumbukan terjadi pada waktu yang relatif sangat singkat. Percepatan gravitasi g = 10 m/s2. Momen inersia bola ping-pong adalah dengan R = jari-jari bola ping-pong. Tentukan energi yang hilang selama tumbukan bola dengan meja.
6.
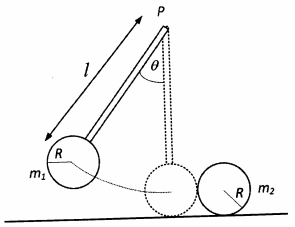
Jawab →Sebuah bandul fisis terdiri atas sebuah cakram berjari-jari R yang bermassa m1 dan sebuah batang tegat yang massanya dapat diabaikan. Cakram diletakan di salah satu ujung batang, sedangkan ujung batang yang lain dapat berputar pada titik P (bayangkan cakram menjadi bandul). Jarak antara titik putar dengan pusat massa bandul adalah l. Mula-mula bandul dilepaskan dari keadaan diam yang membuat sudut cukup kecil terhadap vertikal. Tepat pada posisi terendahnya, bandul menumbuk secara tidak elastis sama sekali cakram yang lain berjari-jari R dan bermassa m2, dengan m2 < m1. Tentukan:
a. periode bandul sebelum tumbukan? (Nyatakan dalam l, g, dan R)
b. kecepatan bandul sesaat sebelum tumbukan? (Nyatakan dalam l, g, dan R)
c. kecepatan bandul sesaat sesudah tumbukan? (Nyatakan dalam m1, m2, l, g, R, dan )
d. periode bandul setelah tumbukan? (Nyatakan dalam l, g, dan R)
7.
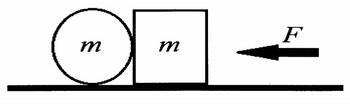
Jawab →Sebuah kubus dan silinder berada pada lantai horisontal kasar. Kedua permukaan benda tersebut saling bersinggungan, seperti pada gambar. Massa kedua benda sama, demikian pula diameter silinder sama dengan panjang sisi kubus. Untuk seluruh permukaan, koefisien gesek statik dan kinetik masing-masing adalah µs, dan µk . Drketahui m = 12 kg, µs = 0,6, µk = 0,2 dan percepatan gravitasi g = 10 rn/s2 .
a. Tentukan besar gaya horisontal F yang harus diberikan pada kubus agar kedua benda tersebut bergerak bersama dimana gerakan silinder adalah translasi murni.
b. Tentukan jenis gerakan sistem mula-mula saat sistem mulai bergerak dari keadaan diam (apakah gerakannya murni translasi, translasi dan rotasi atau lainnya).
c. Tinjau sekarang sistim kubus dan silinder dalam keadaan bergerak. Tentukan jenis gerakan sistem jika gaya horisontal yang diberikan sedikit lebih kecil daripada F (yang dihitung pada soal a). Tentukan pula jenis gerakan sistem jtka gaya horisontal yang diberikan sama dengan 1/2 F.