Olimpiade Sains Provinsi (OSP) 2024 - Komputer
Deskripsi Untuk Soal Nomor 1 dan 4
Studi Kasus A: String Cantik OSN
Deskripsi Cerita
Selamat kepada Anda yang telah lolos ke OSN-P Informatika 2024! Pak Dengklek ingin menyelamati dan juga menyemangati Anda dengan membuatkan Anda sebuah string cantik OSN.
Sebuah string dikatakan string cantik OSN jika dan hanya jika memenuhi 2 persyaratan berikut:
- Memiliki panjang minimal 3 huruf.
- Setiap 3 huruf yang berurutan harus terdiri dari tepat 1 huruf 'O', 1 huruf 'S', dan 1 huruf 'N'.
Pada awalnya, Pak Dengklek memiliki sebuah string awal S. Pak Dengklek boleh menghapus beberapa huruf (mungkin saja nol) dari S dan tetap mempertahankan urutan huruf-huruf yang tidak dihapus. Pak Dengklek ingin string akhir setelah penghapusan tersebut adalah sebuah string cantik OSN, yang kemudian akan diberikan kepada Anda.
Carilah panjang string cantik OSN terpanjang yang mungkin Anda terima! Perlu diperhatikan bahwa bisa jadi Pak Dengklek tidak dapat membuatkan Anda sebuah string cantik OSN dari string awal S.
1.
Jawab →Manakah dari 5 pilihan string berikut yang bukan merupakan string cantik OSN?
- "NSO"
- "SNOS"
- "SONSO"
- "ONSONS"
- "NOSNOSO"
2.
Jawab →Ada berapa banyak string berbeda dengan panjang 100 huruf yang juga merupakan string cantik OSN?
Tuliskan jawaban dalam bentuk ANGKA.
3.
Jawab →BENAR atau SALAH: Diberikan string awal berupa "CONTOHSTRINGUNTUKSOALBENARATAUSALAH", Pak Dengklek dapat membuatkan Anda string cantik OSN berupa "OSNOSN" dari string awal tersebut.
4.
Jawab →STRING CANTIK OSN
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
SFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan panjang string cantik OSN terpanjang yang mungkin Anda terima. Jika Pak Dengklek tidak dapat membuatkan Anda sebuah string cantik OSN dari string awal S, keluarkan -1.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
OSN | 3 |
NASIONAL | 4 |
INFORMATIKA | -1 |
OSNNSONO | 5 |
Penjelasan Contoh:
Pada contoh pertama, string awal sudah merupakan string cantik OSN sehingga merupakan string cantik OSN terpanjang yang mungin Anda terima.
Pada contoh kedua, Pak Dengklek dapat menghapus huruf ke-2, ke-4, ke-7, dan ke-8 sehingga string akhir setelah penghapusan adalah "NSON" yang merupakan sebuah string cantik OSN.
Pada contoh ketiga, Pak Dengklek tidak dapat membuatkan Anda sebuah string cantik OSN karena string tersebut tidak memiliki huruf 'S'.
Pada contoh keempat, Pak Dengklek dapat menghapus huruf ke-2, ke-3, dan ke-8 sehingga string akhir setelah penghapusan adalah "ONSON" yang merupakan sebuah string cantik OSN.
Batasan:
Untuk seluruh kasus uji berlaku:
- 1 ≤ |S| ≤ 100 000, dengan |S| menyatakan panjang dari string S
- S hanya terdiri dari huruf-huruf kapital 'A' hingga 'Z'
Batasan Tambahan untuk Subsoal 1 (Mudah)
Subsoal ini hanya berisi satu buah kasus uji, yaitu sebagai berikut:
OLIMPIADESAINSNASIONALTINGKATPROVINSIBatasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Deskripsi Untuk Soal Nomor 5 dan 8
Studi Kasus B: Berbagi Banyak Candil
Deskripsi Cerita
Pak Dengklek memiliki sekian ekor bebek. Pak Dengklek memberi tahu Anda bahwa ia memiliki setidaknya satu ekor bebek dan paling banyak B ekor bebek.
Pagi hari ini, Pak Dengklek telah membeli C butir jajanan candil untuk dibagikan ke bebek-bebeknya. Pak Dengklek ingin membagikan candil-candil tersebut sebanyak mungkin kepada bebek-bebeknya selama setiap bebeknya mendapatkan banyak butir candil yang sama rata. Setelah membagikan candil-candil tersebut, sisa candil akan dimakan oleh Pak Dengklek.
Pak Dengklek memberitahu Anda bahwa banyaknya candil yang akhirnya ia makan adalah D. Tugas Anda adalah menerka banyaknya bebek milik Pak Dengklek, dengan cara menghitung berapa banyak kemungkinan banyaknya bebek berbeda milik Pak Dengklek yang mungkin. Perhatikan bahwa jawaban bisa saja 0 dikarenakan adanya kekeliruan informasi yang diberikan oleh Pak Dengklek.
5.
Jawab →Asumsikan Pak Dengklek membeli 100 butir candil dan banyaknya candil yang akhirnya dimakan oleh Pak Dengklek adalah 10. Dari 5 skenario berikut, manakah yang sebenarnya tidak mungkin?
- Pak Dengklek memiliki 9 ekor bebek
- Pak Dengklek memiliki 15 ekor bebek
- Pak Dengklek memiliki 18 ekor bebek
- Pak Dengklek memiliki 30 ekor bebek
- Pak Dengklek memiliki 45 ekor bebek
6.
Jawab →Asumsikan Pak Dengklek memiliki paling banyak 100 ekor bebek. Jika Pak Dengklek membeli 20 butir candil dan banyaknya candil yang akhirnya dimakan oleh Pak Dengklek adalah 2, maka berapa banyak kemungkinan banyaknya bebek berbeda milik Pak Dengklek yang mungkin?
Tuliskan jawaban dalam bentuk ANGKA.
7.
Jawab →BENAR atau SALAH: Banyaknya kemungkinan banyaknya bebek berbeda milik Pak Dengklek yang mungkin pasti dijamin kurang dari atau sama dengan banyaknya butir candil yang Pak Dengklek beli.
8.
Jawab →BERBAGI BANYAK CANDIL
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
B C DFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan banyaknya kemungkinan banyaknya bebek berbeda milik Pak Dengklek yang mungkin.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
100 13 3 | 2 |
9 9 0 | 3 |
77 42 42 | 35 |
7 42 42 | 0 |
Penjelasan Contoh:
Pada contoh pertama, hanya 2 dari 100 kemungkinan banyaknya bebek berbeda milik Pak Dengklek yang mungkin, yakni sebanyak 5 atau 10 ekor bebek.
Pada contoh kedua, ada 3 kemungkinan yang mungkin, yakni sebanyak 1, 3, atau 9 ekor bebek.
Pada contoh ketiga, ada 35 kemungkinan yang mungkin, yakni sebanyak 43, 44, hingga 77 ekor bebek.
Pada contoh keempat, berdasarkan penjelasan contoh ketiga, tidak ada kemungkinan yang mungkin.
Batasan:
Untuk seluruh kasus uji berlaku:
- 1 ≤ B, C ≤ 1012
- 0 ≤ D ≤ C
Batasan Tambahan untuk Subsoal 1 (Mudah)
Subsoal ini hanya berisi satu buah kasus uji, yaitu sebagai berikut:
25 8420 20Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan: Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!
Deskripsi Untuk Soal Nomor 9 dan 12
Studi Kasus C: Tebas Tebang Pohon
Deskripsi Cerita
Di belakang rumah Pak Dengklek terdapat N buah pohon yang mana pohon ke-i memiliki ketinggian sebesar Ai. Pak Dengklek berencana untuk menebang pohon-pohon tersebut untuk membangun sebuah kandang untuk bebek-bebeknya.
Cara menebang Pak Dengklek cukup unik yakni sebagai berikut. Pak Dengklek pertama-tama akan menentukan sebuah bilangan bulat non-negatif X yang disebut sebagai batas ketinggian maksimum. Kemudian, Pak Dengklek akan menebang bagian atas seluruh pohon yang memiliki tinggi lebih dari X sehingga pohon tersebut pada akhirnya memiliki ketinggian tepat X. Sehingga, apabila sebuah pohon dengan ketinggian Y ditebang karena Y > X, maka Pak Dengklek akan mendapatkan sebuah potongan pohon dengan panjang Y – X dari pohon tersebut.
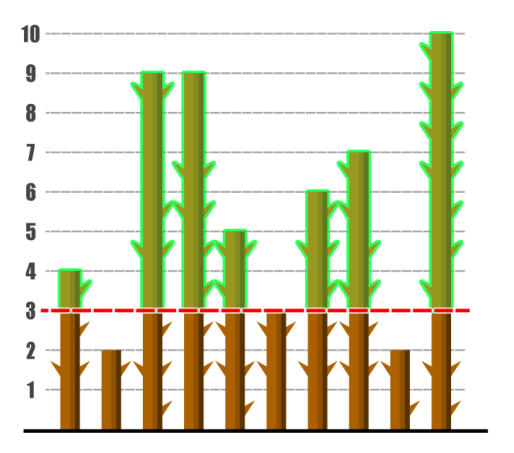
Seluruh potongan pohon yang ditebang akan disatukan dan dijumlahkan panjangnya. Agar Pak Dengklek dapat membangun kandang, Pak Dengklek membutuhkan jumlah panjang potongan pohon yang ditebang yakni setidaknya sebesar M. Karena Pak Dengklek ingin pohon-pohon di belakang rumahnya tetap menjulang tinggi, Pak Dengklek akan memilih batas ketinggian maksimum yang paling tinggi selama ia dapat membangun kandang untuk bebek-bebeknya. Bantulah Pak Dengklek!
9.
Jawab →Asumsikan terdapat 20 pohon dengan ketinggian sebesar 1, 2, 3, dan seterusnya hingga 20. Apabila Pak Dengklek menebang dengan batas ketinggian maksimum sebesar 7, maka berapa jumlah panjang potongan pohon yang ditebang oleh Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
10.
Jawab →BENAR atau SALAH: Untuk setiap kemungkinan pohon-pohon di belakang rumah Pak Dengklek, apabila Pak Dengklek dapat membangun sebuah kandang jika ia menebang dengan batas ketinggian maksimum sebesar Z dengan Z > 0, maka Pak Dengklek juga pasti dapat membangun sebuah kandang jika ia menebang dengan batas ketinggian maksimum sebesar Z – 1.
11.
Jawab →Asumsikan terdapat 10 pohon dengan ketinggian sebesar 10, 20, 30, dan seterusnya hingga 100. Apabila Pak Dengklek membutuhkan minimal jumlah panjang potongan pohon yang ditebang sebesar 111, berapakah batas ketinggian maksimum yang paling tinggi yang dapat dipilih oleh Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
12.
TEBAS TEBANG POHON
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
N M
A1 A2 ... ANFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan batas ketinggian maksimum yang paling tinggi yang dapat dipilih oleh Pak Dengklek sehingga ia tetap dapat membangun sebuah kandang untuk bebek-bebeknya. Jika Pak Dengklek tidak mungkin dapat membangun sebuah kandang untuk bebek-bebeknya berapa pun batas ketinggian maksimum yang ia pilih, keluarkan -1.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
10 25 4 2 9 9 5 3 6 7 2 10 | 3 |
5 5 2 7 2 9 5 | 5 |
5 25 2 7 2 9 5 | 0 |
5 125 2 7 2 9 5 | -1 |
Penjelasan Contoh:
Pada contoh pertama, penebangan pohon Pak Dengklek dapat disimak kembali pada ilustrasi pada deskripsi cerita. Jumlah panjang potongan adalah 1+6+6+2+3+4+7 = 29 sehingga cukup bagi Pak Dengklek untuk membangun kandang.
Pada contoh kedua, Pak Dengklek dapat memilih batas ketinggian maksimum sebesar 5, sehingga ia akan menebang pohon ke-2 dan mendapatkan sebuah potongan sepanjang 7 – 5 = 2 serta menebang pohon ke-4 dan mendapatkan sebuah potongan sepanjang 9 – 5 = 4. Jumlah panjang potongan adalah 2+4 = 6 sehingga cukup bagi Pak Dengklek untuk membangun kandang.
Pada contoh ketiga, perhatikan bahwa Pak Dengklek bisa saja memilih batas ketinggian maksimum sebesar 0, yang artinya Pak Dengklek akan menebang habis seluruh pohon untuk membangun kandang.
Pada contoh keempat, bagaimana pun Pak Dengklek menebang pohon-pohon di belakang rumahnya, ia tetap tidak dapat membangun sebuah kandang untuk bebek-bebeknya.
Batasan:
Untuk seluruh kasus uji berlaku:
- 1 ≤ N ≤ 100 000
- 1 ≤ M ≤ 1012
- 1 ≤ Ai ≤ 1 000 000
Batasan Tambahan untuk Subsoal 1 (Mudah)
Pada subsoal ini, untuk seluruh kasus uji berlaku:
- N ≤ 1000
- Ai ≤ 1000
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan: Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!
Deskripsi Untuk Soal Nomor 13 dan 16
Studi Kasus D: Kalkulator Pengubah Basis
Deskripsi Cerita
Pak Dengklek memiliki sebuah kalkulator pengubah basis. Untuk menggunakan kalkulator ini, Pak Dengklek pada awalnya menuliskan sebuah bilangan bulat non-negatif X dalam basis 10. Pak Dengklek kemudian memerintahkan kalkulator tersebut untuk mengubah nilai X ke dalam basis B. Secara cepat, kalkulator tersebut akan menampilkan sebuah string Y tanpa leading zeroes* yang seharusnya merupakan nilai X dalam basis B.
Namun, sangat disayangkan bahwa kalkulator tersebut tidak dapat menampilkan digit selain '0' hingga '9'. Untuk digit di atas '9', kalkulator tersebut akan menuliskan nilai digit tersebut dalam basis 10 tanpa leading zeroes. Misalnya, digit 'A' akan dituliskan sebagai "10", digit 'B' akan dituliskan sebagai "11", dan seterusnya.
Sebagai contoh, Pak Dengklek pada awalnya menuliskan X = 123 456. Pak Dengklek kemudian memerintahkan kalkulator tersebut untuk mengubahnya ke dalam basis B = 16. Bilangan 123 456 dalam basis 16 seharusnya adalah "1E240", namun kalkulator tersebut malah akan menampilkan Y = "114240".
Pak Dengklek kemudian secara cermat mengamati bahwa bisa jadi akan ada banyak bilangan berbeda, yang jika diubah ke dalam suatu basis yang sama, akan menampilkan hasil yang sama pula. Misalnya, 737 856 dalam basis 16 juga akan ditampilkan sebagai "114240". Pun demikian 1 131 072 dalam basis 16 juga akan ditampilkan sebagai "114240".
Diberikan nilai B dan Y, tugas Anda adalah menghitung banyaknya X berbeda, sehingga apabila X diubah ke dalam basis B, maka kalkulator akan menampilkan hasil berupa string Y. Karena jawabannya bisa sangat besar, keluarkan jawabannya modulo 1 000 000 007.
*) Sebagai catatan, sebuah string tidak memiliki leading zeroes apabila digit pertama bukan '0' kecuali jika bilangan tersebut memang 0. Sebagai contoh, "42", "0", dan "1000" merupakan bilangan-bilangan tanpa leading zeroes.
13.
Jawab →Apabila Pak Dengklek memerintahkan kalkulatornya untuk mengubah nilai 15 015 ke dalam basis 13, maka string apa yang akan ditampilkan oleh kalkulator?
Tuliskan jawaban dalam bentuk STRING tanpa tanda petik.
14.
Jawab →Asumsikan Pak Dengklek mengubah suatu bilangan ke dalam basis 14 dan kalkulator menampilkan hasil berupa string "123010". Dari 5 skenario berikut, manakah yang tidak mungkin?
- Angka yang diubah ke dalam basis 14 oleh Pak Dengklek adalah 33 526
- Angka yang diubah ke dalam basis 14 oleh Pak Dengklek adalah 44 502
- Angka yang diubah ke dalam basis 14 oleh Pak Dengklek adalah 44 506
- Angka yang diubah ke dalam basis 14 oleh Pak Dengklek adalah 469 238
- Angka yang diubah ke dalam basis 14 oleh Pak Dengklek adalah 622 902
15.
Jawab →Berapa banyak bilangan berbeda yang jika diubah ke dalam basis 16 maka kalkulator akan menampilkan hasil berupa string "71112016"?
Tuliskan jawaban dalam bentuk ANGKA.
16.
Jawab →KALKULATOR PENGUBAH BASIS
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
B
YFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan banyaknya X berbeda, sehingga apabila X diubah ke dalam basis B, maka kalkulator akan menampilkan hasil berupa string Y, modulo 1 000 000 007.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
16 114240 | 3 |
4 114240 | 0 |
10 0 | 1 |
10 1001 | 1 |
1000000 12345678912345678912345678912345678 | 649774399 |
Penjelasan Contoh:
Pada contoh pertama, terdapat 3 kemungkinan X berbeda, yakni 123 456, 737 856, dan 1 131 072; seperti yang telah dijelaskan pada deskripsi cerita.
Pada contoh kedua, tidak ada nilai X yang mungkin karena setiap bilangan yang diubah ke basis 4 pasti hanya memiliki digit 0, 1, 2, atau 3.
Pada contoh ketiga, hanya ada 1 kemungkinan X, yakni 0.
Pada contoh keempat, hanya ada 1 kemungkinan X, yakni 1001.
Pada contoh kelima, sebenarnya terdapat 26 649 774 581 kemungkinan X berbeda, namun perhatikan bahwa jawaban harus dalam modulo 1 000 000 007.
Batasan:
Untuk seluruh kasus uji berlaku:
- 2 ≤ B ≤ 1 000 000
- 1 ≤ |Y| ≤ 100 000, dengan |Y| menyatakan panjang dari string Y
- Y hanya terdiri dari digit-digit '0' hingga '9' dan tidak memiliki leading zeroes
Batasan Tambahan untuk Subsoal 1 (Mudah)
Pada subsoal ini, untuk seluruh kasus uji berlaku:
- B ≤ 16
- |Y| ≤ 6
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Deskripsi Untuk Soal Nomor 17 dan 20
Studi Kasus E: Gosip Gulali
Deskripsi Cerita
Pak Dengklek memiliki N ekor bebek penggemar gulali, yang dinomori dari 1 hingga N. Untuk liburan akhir tahun ini, Pak Dengklek ingin memberi hadiah kepada mereka berupa gulali. Terdapat M jenis gulali yang dapat dibeli oleh Pak Dengklek, dinomori dari 1 hingga M. Jenis gulali ke-i memiliki tingkat kemanisan sebesar Gi. Perhatikan bahwa Pak Dengklek boleh membeli sebuah jenis gulali yang sama beberapa kali, atau dengan kata lain, setiap jenis gulali memiliki stok gulali yang tidak terbatas.
Setiap bebek Pak Dengklek memiliki tingkat kemanisan favoritnya masing-masing. Bebek ke-i memiliki tingkat kemanisan favorit sebesar Bi. Idealnya, mereka ingin mendapatkan gulali dengan tingkat kemanisan yang tepat sama dengan tingkat kemanisan favorit mereka. Namun, mereka akan tetap menerima gulali dengan tingkat kemanisan berapa pun juga, meskipun mungkin akan timbul rasa ketidakpuasan. Apabila seekor bebek memiliki tingkat kemanisan favorit X dan ia mendapatkan gulali dengan tingkat kemanisan Y, maka rasa ketidakpuasan bebek tersebut dapat dinyatakan sebagai selisih dari X dan Y.
Lebih lanjut, ternyata para bebek suka bergosip dengan teman-temannya. Seekor bebek mungkin bergosip dengan nol atau lebih bebek lain. Diketahui bahwa terdapat K buah hubungan gosip. Setiap hubungan gosip dinyatakan sebagai dua buah bilangan bulat berbeda Pi dan Qi yang artinya bebek ke-Pi dan bebek ke-Qi saling bergosip satu sama lain.
Apabila bebek ke-A bergosip dengan bebek ke-B, maka bebek ke-A pasti akan tahu jenis gulali yang diterima oleh bebek ke-B, dan sebaliknya. Apabila bebek ke-A bergosip dengan bebek ke-B, dan bebek ke-B juga bergosip dengan bebek ke-C, maka bebek ke-A juga akan mulai bergosip dengan bebek ke-C. Alhasil, bebek ke-A juga pasti akan tahu jenis gulali yang diterima oleh bebek ke-C, dan juga sebaliknya.
Agar mencegah terjadinya rasa iri antar para bebek, Pak Dengklek akan menjamin bahwa jika bebek ke-A mengetahui jenis gulali yang diterima oleh bebek ke-B, maka bebek ke-A harus mendapatkan gulali dengan jenis yang sama dengan bebek ke-B. Jika dua bebek tidak saling mengetahui jenis gulali yang diterima oleh yang lain, maka kedua bebek boleh saja mendapatkan gulali yang sama atau pun berbeda jenis.
Tentunya, Pak Dengklek ingin membuat seluruh bebek-bebeknya sesenang mungkin, sehingga ia ingin mencari cara untuk memberikan gulali ke semua bebek-bebeknya sedemikian sehingga total rasa ketidakpuasan dari semua bebek-bebeknya sekecil mungkin. Bantulah Pak Dengklek!
17.
Asumsikan bahwa bebek-bebek Pak Dengklek tidak saling bergosip satu sama lain. Misalkan terdapat 5 ekor bebek dengan tingkat kemanisan favorit masing-masing adalah 10, 20, 30, 40, dan 50; dan ada 15 jenis gulali dengan tingkat kemanisan masing-masing sebesar 3, 6, 9, dan seterusnya hingga 45. Berapa total rasa ketidakpuasan terkecil yang dapat diperoleh oleh bebek-bebek Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
18.
Jawab →Asumsikan ada 4 ekor bebek bernama Kwak, Kwik, Kwuk dan Kwok. Tingkat kemanisan favorit mereka secara berturut-turut adalah 8, 6, 1, dan 3. Diketahui bahwa pasangan Kwak-Kwok dan Kwuk-Kwok saling bergosip satu sama lain. Jika ada 3 jenis gulali dengan tingkat kemanisan secara berturut-turut sebesar 4, 2, dan 9; berapa total rasa ketidakpuasan terkecil yang dapat diperoleh oleh mereka?
Tuliskan jawaban dalam bentuk ANGKA.
19.
Jawab →BENAR atau SALAH: Asumsikan untuk seluruh bilangan bulat positif X, selalu terdapat jenis gulali dengan tingkat kemanisan sebesar X pula. Apabila terdapat 3 ekor bebek yang harus mendapatkan gulali dengan jenis yang sama, maka pasti optimal untuk memberi mereka jenis gulali dengan tingkat kemanisan yang sedekat mungkin dengan nilai rata-rata tingkat kemanisan favorit mereka bertiga.
20.
GOSIP GULALI
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 3 detik dan memory limit sebanyak 256 MB.
Format Masukan:
N M K
B1 B2 ... BN
G1 G2 ... GM
P1 Q1
P2 Q2
...
PK QKFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan total rasa ketidakpuasan terkecil yang dapat diperoleh oleh bebek-bebek Pak Dengklek.
Contoh Masukan dan Keluaran:
Contoh Masukan | Contoh Keluaran |
|---|---|
| |
| |
Penjelasan Contoh:
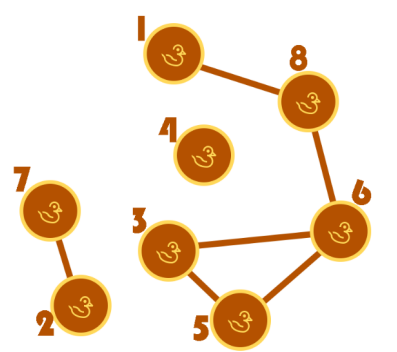
Pada contoh pertama, hubungan-hubungan gosip dapat diilustrasikan sebagai berikut.

Salah satu cara Pak Dengklek meminimalkan total rasa ketidakpuasan yakni dengan memberi gulali dengan tingkat kemanisan 50 kepada bebek ke-1, ke-3, ke-5, ke-6, dan ke-8; 30 kepada grup bebek ke-2 dan ke-7, serta 40 kepada bebek ke-4. Dapat dihitung bahwa total rasa ketidakpuasan adalah 150.
Pada contoh kedua, meskipun keempat bebek boleh mendapatkan gulali yang berbeda-beda jenis, Pak Dengklek dapat memberi keempatnya gulali dengan tingkat kemanisan 10 untuk meminimalkan total rasa ketidakpuasan, yaitu sebesar |1 – 10| + |2 – 10| + |13 – 10| + |14 – 10| = 24.
Batasan:
Untuk seluruh kasus uji berlaku:
1 ≤ N, M ≤ 100 000
0 ≤ K ≤ 100 000
1 ≤ Bi, Gi ≤ 109
dan pasangan-pasangan (Pi, Qi) saling berbeda satu sama lain
Batasan Tambahan untuk Subsoal 1 (Mudah)
Pada subsoal ini, untuk seluruh kasus uji berlaku:
M ≤ 10
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan: Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!
Deskripsi Untuk Soal Nomor 21 dan 24
Studi Kasus F: Maju Tak Papan
Deskripsi Cerita
Pak Dengklek memiliki papan berukuran N baris dan M kolom. Setiap baris dinomori dari 1 hingga N dari atas ke bawah dan setiap kolom dinomori dari 1 hingga M dari kiri ke kanan. Petak (X, Y) menyatakan petak pada baris ke-X dan kolom ke-Y. Pak Dengklek akan mengisi setiap petak pada papan tersebut dengan angka 1 hingga N × M sedemikian sehingga masing-masing angka akan muncul tepat satu kali pada papan.
Sebuah robot bebek akan mulai pada petak (1, 1). Pada setiap waktu, robot tersebut akan membandingkan petak tepat di kanannya dengan petak tepat di bawahnya. Robot kemudian akan berpindah ke petak yang memiliki angka yang lebih besar. Jika robot berada pada baris terakhir (baris ke-N), maka ia secara otomatis hanya akan bergerak ke kanan. Jika robot berada pada kolom terakhir (kolom ke-M), maka ia secara otomatis hanya akan bergerak ke bawah. Robot akan berhenti pada petak (N, M).
Angka-angka pada seluruh petak yang dikunjungi oleh robot bebek (termasuk petak (1, 1) dan petak (N, M)) akan dijumlahkan. Pak Dengklek kemudian akan memberi hadiah kepada bebek-bebeknya permen sebanyak jumlah ini.
Karena Pak Dengklek tidak ingin bebek-bebeknya makan terlalu banyak permen, tugas Anda adalah membantu Pak Dengklek untuk menentukan jumlah terkecil yang mungkin apabila Pak Dengklek mengisi setiap petak pada papannya dengan angka 1 hingga N × M secara optimal.
21.
Jawab →Asumsikan papan Pak Dengklek berukuran 3 baris dan 4 kolom dan Pak Dengklek mengisi papan tersebut dengan konfigurasi angka-angka seperti berikut ini.
| 4 | 6 | 1 | 10 |
| 3 | 5 | 8 | 9 |
| 12 | 11 | 2 | 7 |
Berapa jumlah angka-angka pada petak-petak yang akan dikunjungi oleh robot bebek?
Tuliskan jawaban dalam bentuk ANGKA.
22.
Jawab →Apabila papan Pak Dengklek berukuran 5 baris dan 2 kolom, berapa jumlah terkecil yang mungkin apabila Pak Dengklek mengisi setiap petak pada papan dengan angka 1 hingga 10 secara optimal?
Tuliskan jawaban dalam bentuk ANGKA.
23.
Jawab →Apabila papan Pak Dengklek berukuran 3 baris dan 3 kolom, berapa jumlah terkecil yang mungkin apabila Pak Dengklek mengisi setiap petak pada papan dengan angka 1 hingga 9 secara optimal?
Tuliskan jawaban dalam bentuk ANGKA.
24.
Jawab →MAJU TAK PAPAN
Tulislah sebuah program dengan bahasa C/C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
N MFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan jumlah terkecil yang mungkin apabila Pak Dengklek mengisi setiap petak pada papannya dengan angka 1 hingga N × M secara optimal.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
2 3 | 11 |
1 1 | 1 |
Penjelasan Contoh:
Pada contoh pertama, salah satu konfigurasi pengisian yang optimal adalah sebagai berikut.
| 2 | 4 | 6 |
| 5 | 3 | 1 |
Robot bebek akan berjalan sebagai berikut:
- Robot mulai pada petak (1, 1) yang berisi angka 2.
- Antara petak kanan (1, 2) yang berisi angka 4 dan petak bawah (2, 1) yang berisi angka 5, petak bawah memiliki angka yang lebih besar, sehingga robot akan bergerak ke bawah.
- Karena robot berada pada baris terakhir, robot secara otomatis akan bergerak ke kanan ke petak (2, 2) yang berisi angka 3.
- Karena robot berada pada baris terakhir, robot secara otomatis akan bergerak ke kanan ke petak (2, 3) yang berisi angka 1.
- Karena robot berada pada petak (N, M), maka robot akan bergenti bergerak.
Jumlah angka-angka pada petak-petak yang dikunjungi oleh robot bebek adalah 2+5+3+1 = 11.
Pada contoh kedua, hanya ada 1 kemungkinan konfigurasi pengisian yakni satu petak berisi angka 1.
Batasan:
Untuk seluruh kasus uji berlaku:
- 1 ≤ N, M ≤ 1000
Batasan Tambahan untuk Subsoal 1 (Mudah)
Pada subsoal ini, untuk seluruh kasus uji berlaku:
- N ≤ 2
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.