Olimpiade Sains Provinsi (OSP) 2025 - Komputer
Deskripsi Untuk Soal Nomor 1 dan 4
Studi Kasus A. String Cantik OSN-P
Selamat kepada Anda yang telah lolos ke OSN-P Informatika 2025! Pak Dengklek ingin menyelamati dan juga menyemangati Anda dengan membuatkan Anda sebuah string cantik OSN-P.
Sebuah string dikatakan string cantik OSN-P jika dan hanya jika memenuhi 2 persyaratan berikut:
- Hanya terdiri dari huruf ‘O’, ‘S’, ‘N’, dan ‘P’; serta masing-masing harus muncul minimal satu kali.
- Tidak boleh terdapat huruf selain ‘P’ setelah huruf ‘P’.
Pada awalnya, Pak Dengklek memiliki sebuah string awal S. Pak Dengklek boleh menghapus beberapa huruf (mungkin saja nol) dari S dan tetap mempertahankan urutan huruf-huruf yang tidak dihapus. Pak Dengklek ingin string akhir setelah penghapusan tersebut adalah sebuah string cantik OSN-P.
Carilah panjang string cantik OSN-P terpanjang yang mungkin dibuat! Perlu diperhatikan bahwa bisa jadi Pak Dengklek tidak dapat membuat sebuah string cantik OSN-P dari string awal S.
1.
Jawab →Manakah dari 5 pilihan string berikut yang merupakan string cantik OSN-P?
- “OSN”
- “SSNOSOPP”
- “OSNPOP”
- “NOWOSP”
- “OSOPP”
2.
Jawab →BENAR atau SALAH: Diberikan string awal S = “SOPRANOSATPOLPP”, Pak Dengklek dapat membuat sebuah string cantik OSN-P (tidak harus yang terpanjang) yang terdiri atas tepat 3 huruf ‘P’.
3.
Jawab →Diberikan string awal S = “SOPRANOSATPOLPP”, apa string cantik OSN-P terpanjang yang mungkin dibuat? Jika terdapat lebih dari satu kemungkinan jawaban, pilih yang paling kecil secara leksikografis (muncul paling awal dalam urutan kamus).
Tuliskan jawaban dalam bentuk STRING tanpa tanda petik.
4.
Jawab →STRING CANTIK OSN-P
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
SFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan panjang string cantik OSN-P terpanjang yang mungkin dibuat. Jika Pak Dengklek tidak dapat membuat sebuah string cantik OSN-P dari string awal S, keluarkan -1.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
OSNP | 4 |
INISOPRANOSATPOLPP | 9 |
OSNTINGKATPROVINSI | 5 |
OLIMPIADESAINSNASIONAL | -1 |
Penjelasan Contoh
Pada contoh pertama, string awal sudah merupakan string cantik OSN-P sehingga merupakan string cantik OSN-P terpanjang yang mungkin dibuat.
Pada contoh kedua, Pak Dengklek dapat menghapus nol atau lebih huruf dari string “INISOPRANOSATPOLPP” untuk membuat sebuah string cantik OSN-P sepanjang 9 huruf. Beberapa kemungkinan hasilnya adalah “NSONOSPPP” dan “NSONOSOPP”.
Pada contoh ketiga, string cantik OSN-P terpanjang yang dapat dibuat adalah “OSNNP”.
Pada contoh keempat, Pak Dengklek tidak dapat membuatkan Anda string cantik OSN-P apa pun.
Batasan
- 1 ≤ |S| ≤ 200 000, dengan |S| menyatakan panjang dari string S
- S hanya terdiri dari huruf-huruf kapital ‘A’ hingga ‘Z’
Batasan Tambahan untuk Subsoal 1 (Mudah)
- |S| ≤ 2000
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Deskripsi Untuk Soal Nomor 5 dan 8
Studi Kasus B. Gudang Penyimpanan Kardus
Pak Dengklek ingin membangun sebuah gudang untuk menyimpan kotak-kotak kardus miliknya.
Pak Dengklek memiliki N buah kardus. Setiap kardus memiliki ukuran yang sama yakni panjang P satuan dan lebar L satuan. Kardus-kardus tersebut gampang rapuh, sehingga Pak Dengklek tidak boleh menumpuk sebuah kardus di atas kardus yang lain saat disimpan di dalam gudang.
Pak Dengklek ingin agar gudang yang ia bangun memiliki alas berbentuk persegi. Pak Dengklek ingin seluruh kardus disimpan dengan estetik, yakni memiliki orientasi yang sama dan sejajar sisi-sisi gudang. Dengan kata lain, seluruh panjang kardus harus sejajar dengan sumbu memanjang (kiri-kanan) dan seluruh lebar kardus harus sejajar dengan sumbu melintang (depan-belakang).
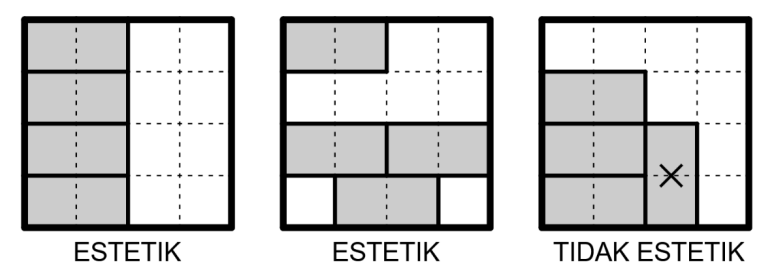
Pak Dengklek ingin mengetahui berapa panjang sisi gudang terkecil yang mungkin sehingga seluruh kardus yang dimiliki oleh Pak Dengklek dapat disimpan di dalam gudang tersebut dengan estetik.
5.
Jawab →Apabila kardus-kardus Pak Dengklek memiliki panjang 17 satuan dan lebar 8 satuan, berapakah paling banyak kardus yang bisa Pak Dengklek simpan di dalam gudang dengan panjang sisi 45 satuan dengan estetik?
Tuliskan jawaban dalam bentuk ANGKA.
6.
Jawab →BENAR atau SALAH: Apabila Pak Dengklek dapat menyimpan seluruh kardus di dalam gudang dengan panjang sisi S satuan dengan estetik, maka Pak Dengklek pasti dapat menyimpan seluruh kardus di dalam gudang dengan panjang sisi S + 1 satuan dengan estetik pula.
7.
Jawab →Apabila Pak Dengklek memiliki 31 kardus dengan panjang 3 satuan dan lebar 1 satuan, maka berapa panjang sisi gudang terkecil sehingga Pak Dengklek dapat menyimpan seluruh kardus dengan estetik?
Tuliskan jawaban dalam bentuk ANGKA.
8.
Jawab →GUDANG PENYIMPANAN KARDUS
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
N P LFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan panjang sisi gudang terkecil sehingga Pak Dengklek dapat menyimpan seluruh kardus dengan estetik.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
17 1 1 | 5 |
1000000000000 2000 2000 | 2000000000 |
4 2 1 | 4 |
1000000000000 4 3 | 3464104 |
Penjelasan Contoh
Pada contoh pertama, meskipun ukuran kardus sangatlah kecil, Pak Dengklek hanya dapat menyimpan paling banyak 16 kardus di dalam sebuah gudang dengan panjang sisi 4 satuan. Sehingga, untuk menyimpan 17 kardus, panjang sisi gudang terkecil yang perlu dibangun adalah 5 satuan.
Pada contoh kedua, perhatikan bahwa gudang bisa saja dipenuhi oleh kardus-kardus Pak Dengklek tanpa menyisakan ruang apa pun.
Pada contoh ketiga, sebenarnya keempat kardus dapat disimpan di dalam gudang dengan panjang sisi 3 satuan apabila tidak harus estetik. Jika harus disusun dengan estetik, Pak Dengklek perlu membangun gudang dengan panjang sisi 4 satuan.
Pada contoh keempat, perhatikan bahwa Anda perlu berhati-hati dengan overflow!
Batasan
- 1 ≤ N ≤ 1012
- 1 ≤ L ≤ P ≤ 2000
Batasan Tambahan untuk Subsoal 1 (Mudah)
- P = L
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan
Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!
Deskripsi Untuk Soal Nomor 9 dan 12
Studi Kasus C. Balada Kemasan Telur
Pak Dengklek ingin berjualan telur dengan modal uang sebesar N rupiah. Di pusat grosir, dijual berbagai tipe telur dalam kemasan persegi. Untuk setiap bilangan prima p, terdapat tipe telur p yang dijual di dalam kemasan berukuran p × p yang berisikan p × p buah telur, dengan harga p rupiah per kemasan. Perhatikan bahwa tidak ada tipe telur k dengan k adalah bilangan non-prima. Diketahui juga bahwa banyaknya stok tiap tipe telur tidak terbatas.
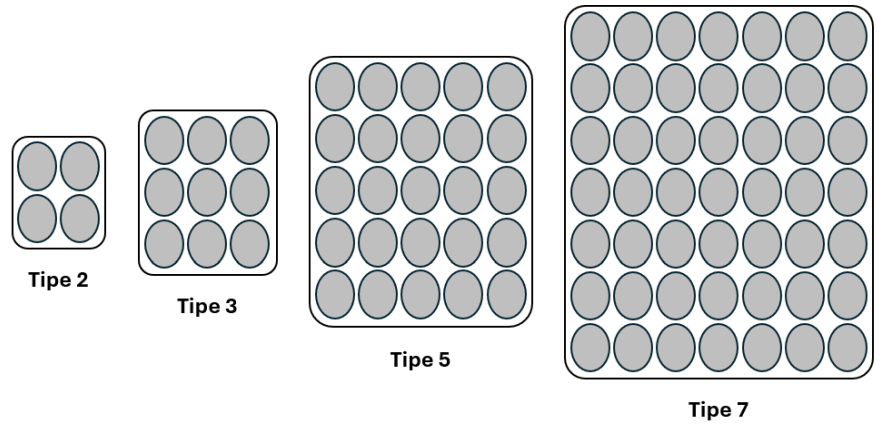
Karena Pak Dengklek tidak mau ribet, Pak Dengklek akan memilih tepat satu tipe telur saja dan membelanjakan seluruh modal uangnya untuk membeli tipe telur tersebut tanpa sisa. Dengan kata lain, Pak Dengklek harus memilih suatu tipe telur p sehingga p habis membagi N.
Setelah pulang dari pusat grosir, Pak Dengklek akan menjual kembali seluruh telur yang ia telah dapatkan. Pak Dengklek akan menyusun seluruh telur di dalam tepat satu kemasan baru berukuran s × t berisikan s × t buah telur.
Sebagai contoh, jika Pak Dengklek sekarang memiliki 36 butir telur, maka terdapat 9 ukuran kemasan yang mungkin: 1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6, 9 × 4, 12 × 3, 18 × 2, dan 36 × 1.
Sayangnya, Pak Dengklek belum tahu ukuran s × t mana yang akan menarik pelanggannya. Untuk itu, dengan modal uangnya, Pak Dengklek akan memilih suatu tipe telur sedemikian sehingga ketika Pak Dengklek menjual kembali seluruh telurnya, banyak kemungkinan kemasan s × t yang mungkin adalah sebanyak-banyaknya. Perhatikan bahwa jika s ≠ t, maka kemasan s × t dianggap berbeda dengan kemasan t × s.
9.
Jawab →Apabila Pak Dengklek pada awalnya memiliki modal uang sebesar 111 111 rupiah, lalu ia memilih tipe telur 7 untuk dibelanjakan, maka berapakah banyak telur yang akan dijual kembali pada akhirnya?
Tuliskan jawaban dalam bentuk ANGKA.
10.
Jawab →Dari 5 skenario berikut, manakah banyak telur yang menghasilkan banyak kemungkinan kemasan yang paling banyak?
- Jika Pak Dengklek menjual kembali 21 × 51 = 10 butir telur
- Jika Pak Dengklek menjual kembali 22 × 52 = 100 butir telur
- Jika Pak Dengklek menjual kembali 22 × 51 = 20 butir telur
- Jika Pak Dengklek menjual kembali 23 × 51 = 40 butir telur
- Jika Pak Dengklek menjual kembali 26 × 50 = 64 butir telur
11.
Jawab →Apabila Pak Dengklek pada awalnya memiliki modal uang sebesar 45 rupiah, maka tipe telur apakah yang perlu Pak Dengklek pilih agar ketika ia menjual kembali seluruh telurnya, banyak kemungkinan kemasan yang mungkin adalah sebanyak-banyaknya? Jika terdapat lebih dari satu kemungkinan jawaban, pilih yang paling kecil.
Tuliskan jawaban dalam bentuk ANGKA.
12.
BALADA KEMASAN TELUR
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
NFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan tipe telur yang perlu Pak Dengklek pilih agar ketika ia menjual kembali seluruh telurnya, banyak kemungkinan kemasan yang mungkin adalah sebanyak-banyaknya. Jika terdapat lebih dari satu kemungkinan jawaban, pilih yang paling kecil.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
18 | 2 |
60 | 3 |
1000000007 | 1000000007 |
Penjelasan Contoh
Pada contoh pertama, untuk dapat membelanjakan seluruh modal uangnya, Pak Dengklek boleh memilih tipe telur 2 atau 3.
- Apabila Pak Dengklek memilih tipe telur 2, maka Pak Dengklek akan membeli 18 ÷ 2 = 9 kemasan yang masing-masing berisi 2 × 2 = 4 telur, sehingga ia akan memiliki 9 × 4 = 36 telur. Saat Pak Dengklek ingin menjual kembali seluruh telurnya, terdapat 9 kemungkinan kemasan yang mungkin: ukuran 1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6, 9 × 4, 12 × 3, 18 × 2, dan 36 × 1.
- Apabila Pak Dengklek memilih tipe telur 3, maka Pak Dengklek akan membeli 18 ÷ 3 = 6 kemasan yang masing-masing berisi 3 × 3 = 9 telur, sehingga ia akan memiliki 6 × 9 = 54 telur. Saat Pak Dengklek ingin menjual kembali seluruh telurnya, terdapat 8 kemungkinan kemasan yang mungkin: ukuran 1 × 54, 2 × 27, 3 × 18, 6 × 9, 9 × 6, 18 × 3, 27 × 2, dan 54 × 1.
Dengan demikian, untuk mendapatkan kemungkinan kemasan yang paling banyak, Pak Dengklek perlu memilih tipe telur 2.
Pada contoh kedua, untuk dapat membelanjakan seluruh modal uangnya, Pak Dengklek boleh memilih tipe telur 2, 3, atau 5. Dapat dihitung bahwa dengan membeli tipe telur 2, akan ada 16 kemungkinan kemasan yang mungkin; sedangkan dengan membeli tipe telur 3 ataupun 5, akan ada 18 kemungkinan kemasan yang mungkin. Karena terdapat lebih dari satu kemungkinan jawaban yang menghasilkan kemungkinan terbanyak yakni 18, Pak Dengklek akan memilih yang paling kecil yakni 3.
Pada contoh ketiga, perhatikan bahwa N = 1 000 000 007 adalah bilangan prima sehingga Pak Dengklek hanya dapat memilih tipe telur 1 000 000 007.
Batasan
- 2 ≤ N ≤ 1012
Batasan Tambahan untuk Subsoal 1 (Mudah)
- N ≤ 2000
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan
Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!
Deskripsi Untuk Soal Nomor 13 dan 16
Studi Kasus D. Telur Kemasan Balado
Setelah menjadi juragan telur, Pak Dengklek ingin mengembangkan usahanya untuk berjualan telur rebus kemasan. Ada dua varian telur milik Pak Dengklek: varian Asli yakni telur tanpa bumbu apa pun, dan varian Balado yang merupakan telur dengan bumbu pedas.
Pak Dengklek sudah memproduksi N telur yang ditata dari kiri ke kanan. Penataan tersebut dapat direpresentasikan sebagai sebuah string S sepanjang N yang hanya terdiri dari huruf ‘A’ dan ‘B’. Huruf ‘A’ menunjukkan telur varian Asli, sedangkan huruf ‘B’ menunjukkan telur varian Balado.
Suatu hari, Pak Dengklek mendapatkan kabar bahwa Raja Bebek ingin memborong seluruh telur milik Pak Dengklek. Namun, Raja Bebek hanya ingin membeli telur varian Balado saja. Alhasil, Pak Dengklek ingin menyembunyikan nol atau lebih telur dengan operasi berikut:
Pak Dengklek akan memilih telur terkiri (sebut saja telur pada posisi l) dan telur terkanan (sebut saja telur pada posisi r) yang akan disembunyikan.
Pak Dengklek akan menyembunyikan seluruh telur yang berada pada rentang tersebut (dari posisi l hingga r inklusif).
Pak Dengklek akan menata ulang telur-telur sisanya menjadi satu kesatuan dari kiri ke kanan tanpa mengubah urutannya.
Dengan waktu yang tersisa, Pak Dengklek dapat melakukan operasi di atas paling banyak sebanyak K kali (mungkin saja tidak sama sekali). Pada akhirnya, Pak Dengklek harus menjamin bahwa seluruh telur yang tersisa adalah telur varian Balado.
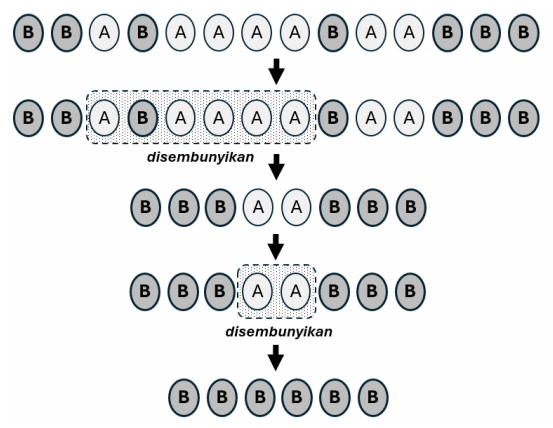
Bantulah Pak Dengklek untuk menentukan paling banyak telur varian Balado yang mungkin dapat Raja Bebek borong!
13.
Jawab →Apabila Pak Dengklek hanya boleh melakukan operasi penyembunyian paling banyak 1 kali, manakah dari 5 pilihan string S berikut yang memungkinkan Raja Bebek memborong telur varian Balado paling banyak?
- “BBBBB”
- “BBAABBBB”
- “AAAAABBBB”
- “BABBBBBBBBAB”
- “AABBBAABABBBABBB”
14.
Jawab →Apabila penataan telur direpresentasikan dengan string “BAABBBAAAABBBBAAABBA”, dengan melakukan operasi penyembunyian paling banyak 2 kali, berapakah banyaknya telur varian Balado terbanyak yang mungkin dapat Raja Bebek borong?
Tuliskan jawaban dalam bentuk ANGKA.
15.
Jawab →Apabila penataan telur direpresentasikan dengan string “BAABBBAAAABBBBAAABBA”, dengan melakukan operasi penyembunyian paling banyak 3 kali, berapakah banyaknya telur varian Balado terbanyak yang mungkin dapat Raja Bebek borong?
Tuliskan jawaban dalam bentuk ANGKA.
16.
Jawab →TELUR KEMASAN BALADO
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 2 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
N K
SFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan banyaknya telur varian Balado terbanyak yang mungkin dapat Raja Bebek borong.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
14 2 BBABAAAABABBB | 6 |
14 4 BBABAAAABABBB | 7 |
4 1000000000 BBBB | 4 |
4 1000000000 AAAA | 0 |
Penjelasan Contoh
Pada contoh pertama, Pak Dengklek dapat melakukan penyembunyian telur seperti pada deskripsi cerita agar Raja Bebek dapat memborong 6 telur varian Balado.
Pada contoh kedua, Pak Dengklek dapat melakukan penyembunyian telur sebagai berikut:
- Dari “BBABAAAABABBB”, sembunyikan telur di posisi 6 hingga 7, tersisa “BBABAABAABBB”.
- Dari “BBABAABAABBB”, sembunyikan telur di posisi 5 hingga 6, menyisakan “BBABBAABBB”.
- Dari “BBABBAABBB”, sembunyikan telur di posisi 3 hingga 3, menyisakan “BBBBBAABBB”.
- Dari “BBBBBAABBB”, sembunyikan telur di posisi 5 hingga 6, menyisakan “BBBBBBB”.
Pada contoh ketiga, karena seluruh telur merupakan varian Balado, Pak Dengklek tidak perlu menyembunyikan telur apa pun.
Pada contoh keempat, karena seluruh telur merupakan varian Asli, Pak Dengklek hanya dapat menyembunyikan seluruhnya sehingga Raja Bebek tidak dapat memborong apa pun.
Batasan
- 1 ≤ N ≤ 200 000
- 1 ≤ K ≤ 109
- S memiliki panjang N dan hanya terdiri dari huruf ‘A’ dan ‘B’
Batasan Tambahan untuk Subsoal 1 (Mudah)
- N ≤ 16
- K ≤ 2
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Deskripsi Untuk Soal Nomor 17 dan 20
Studi Kasus E. Tebas Tebang Bambu
Di belakang rumah Pak Dengklek terdapat N bilah bambu. Bambu ke-i memiliki panjang sebesar Ai satuan. Pak Dengklek berencana untuk menjual seluruh bambunya.
Saat Pak Dengklek ingin berjualan di pasar, diketahui bahwa pelanggan tidak mau membeli bambu secara eceran. Pelanggan hanya mau membeli bambu dalam satuan ikat yang memenuhi dua syarat berikut:
- Setiap ikat bambu harus terdiri dari setidaknya M bilah bambu.
- Setiap bambu dalam satu ikat yang sama harus memiliki panjang yang sama.
Perhatikan bahwa boleh jadi dua atau lebih ikat bambu yang berbeda memiliki panjang bambu yang sama.
Pak Dengklek ingin mengelompokkan seluruh bambunya ke dalam satu atau lebih ikat. Untuk memenuhi kedua syarat di atas, Pak Dengklek dapat memangkas setiap bambunya sehingga panjangnya berkurang. Untuk mempertahankan kekokohan bambu, Pak Dengklek dapat memangkas setiap bambu agar panjangnya berkurang maksimal sepanjang K satuan.
Perhatikan bahwa bagian bambu yang terpangkas tidak dapat digunakan kembali. Perhatikan juga bahwa setiap bambu hanya boleh dipangkas, dan tidak boleh dibelah menjadi lebih dari satu bilah.
Apabila Pak Dengklek harus menjual seluruh bambunya, berapakah banyak ikat maksimum yang dapat ia jual? Perlu diperhatikan bahwa bisa jadi Pak Dengklek tidak dapat menjual seluruh bambunya.
17.
Jawab →Apabila Pak Dengklek tidak dapat memangkas bambu-bambunya (dengan kata lain, nilai K = 0) dan setiap ikat bambu harus terdiri dari setidaknya 3 bilah bambu, manakah dari 5 skenario berikut yang memungkinkan Pak Dengklek untuk menjual seluruh bambunya dan dengan banyaknya ikat bambu yang dijual paling banyak?
- Pak Dengklek akan menjual 14 bilah bambu dengan panjang [1, 2, 3, 4, 5, 6, 7, 7, 6, 5, 4, 3, 2, 1]
- Pak Dengklek akan menjual 14 bilah bambu dengan panjang [2, 3, 4, 2, 3, 4, 2, 3, 4, 2, 3, 4, 2, 3]
- Pak Dengklek akan menjual 14 bilah bambu dengan panjang [5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8]
- Pak Dengklek akan menjual 14 bilah bambu dengan panjang [8, 7, 8, 7, 8, 7, 8, 7, 8, 7, 8, 7, 8, 7]
- Pak Dengklek akan menjual 14 bilah bambu dengan panjang [1, 1, 1, 2, 3, 3, 3, 4, 5, 5, 5, 6, 6, 6]
18.
Jawab →BENAR atau SALAH: Pada kasus-kasus yang memungkinkan Pak Dengklek untuk menjual seluruh bambu, maka untuk memaksimumkan banyaknya ikat bambu yang dapat Pak Dengklek jual, setiap ikat bambu pasti terdiri dari kurang dari 2 × M bilah bambu.
19.
Jawab →Pak Dengklek akan menjual 18 bilah bambu dengan panjang sebagai berikut:
[1, 1, 3, 3, 4, 5, 6, 7, 8, 9, 9, 13, 13, 14, 14, 14, 15, 16]
Apabila Pak Dengklek dapat memangkas bambu-bambunya agar panjangnya berkurang paling banyak 2 satuan, maka berapakah banyaknya ikat bambu maksimum yang dapat Pak Dengklek jual jika setiap ikat bambu harus terdiri dari setidaknya 3 bilah bambu dan Pak Dengklek harus menjual seluruh bambunya?
Jika ternyata tidak mungkin menjual seluruh bambunya, jawablah dengan -1.
Tuliskan jawaban dalam bentuk ANGKA.
20.
Jawab →TEBAS TEBANG BAMBU
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 3 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
N M K
A_1 A_2 ... A_NFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan banyaknya ikat bambu maksimum yang dapat Pak Dengklek jual apabila harus menjual seluruh bambunya. Jika Pak Dengklek tidak mungkin menjual seluruh bambunya, keluarkan -1.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
9 3 0 2 5 3 5 6 5 3 5 2 | -1 |
9 3 1 2 5 3 5 6 5 3 5 2 | 2 |
9 3 3 2 5 3 5 6 5 3 5 2 | 3 |
Penjelasan Contoh
Pada contoh pertama, Pak Dengklek tidak dapat memangkas bambu-bambunya. Alhasil, ia hanya dapat membuat 1 ikat bambu saja berisikan 3 atau 4 bilah bambu dengan panjang 5. Namun, Pak Dengklek tidak dapat menjual seluruh bambunya karena bambu-bambu lainnya tidak dapat membentuk ikat bambu. Oleh karena itu, keluarannya adalah -1.
Pada contoh kedua, Pak Dengklek dapat memangkas bambu ke-3, ke-5, dan ke-7 sehingga panjang tiap bambu secara berturut-turut menjadi [2, 5, 2, 5, 5, 5, 2, 5, 2]. Pak Dengklek kemudian dapat membuat 2 ikat bambu: satu berisikan 4 bilah bambu dengan panjang 2, dan satu lagi berisikan 5 bilah bambu dengan panjang 5. Perhatikan bahwa dengan menjual 2 ikat bambu tersebut, Pak Dengklek akan menjual seluruh bambunya.
Pada contoh ketiga, Pak Dengklek bisa saja memangkas bambu ke-2 hingga ke-8 sehingga panjang tiap bambu secara berturut-turut menjadi [2, 4, 2, 2, 4, 4, 2, 2, 2]. Pak Dengklek kemudian dapat membuat 3 ikat bambu: dua ikat masing-masing berisikan 3 bilah bambu dengan panjang 2, dan satu lagi berisikan 3 bilah bambu dengan panjang 4.
Batasan
- 2 ≤ M ≤ N ≤ 200 000
- 0 ≤ K ≤ 109
- 1 ≤ Ai ≤ 109
Batasan Tambahan untuk Subsoal 1 (Mudah)
- M ≤ 20
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Deskripsi Untuk Soal Nomor 21 dan 24
Studi Kasus F. Kandang Ayam Kandang Bebek
Selain beternak bebek, Pak Dengklek juga sekarang beternak ayam. Seluruh ayam dan bebek tersebut berada di dalam pekarangan yang sama berbentuk segiempat berukuran 2 baris dan N kolom. Baris atas dinomori 1 dan baris bawah dinomori 2. Dari kiri ke kanan, kolom-kolom pekarangan dinomori dari 1 hingga N. Petak pada baris x dan kolom y direpresentasikan dengan (x, y).
Kondisi hewan di pekarangan dinyatakan dengan dua buah string, S1 dan S2, sepanjang N yang masing-masing hanya terdiri dari karakter ‘A’, ‘B’, dan ‘.’ (titik). Karakter ke-j pada Si menunjukkan hewan yang mungkin ada pada petak (i, j). Karakter ‘A’ menunjukkan seekor ayam, karakter ‘B’ menunjukkan seekor bebek, dan karakter ‘.’ menunjukkan ketiadaan hewan.
Selain itu, kondisi lahan pekarangan juga dinyatakan dengan sebuah matriks M berukuran 2 × N berisi bilangan bulat positif. Mi,j menyatakan nilai kebecekan lahan pada petak (i, j).
Pak Dengklek juga memiliki sebuah kandang ayam dan sebuah kandang bebek tepat di sebelah kiri pekarangan. Untuk mudahnya, kandang ayam dapat dianggap terletak pada petak (1, 0) dan kandang bebek terletak pada petak (2, 0). Kandang ayam cukup besar untuk menampung seluruh ayam. Kandang bebek pun cukup besar untuk menampung seluruh bebek.
Pada malam hari, seluruh ayam harus pulang ke kandang ayam dan seluruh bebek pun harus pulang ke kandang bebek. Setiap hewan dapat bergerak 4 arah dari posisinya di petak (i, j): ke atas yakni petak (i − 1, j), ke bawah yakni petak (i + 1, j), ke kiri yakni petak (i, j − 1), atau ke kanan yakni petak (i, j + 1). Perhatikan bahwa mereka tidak boleh keluar dari pekarangan (kecuali ke kandang). Rute yang ditempuh oleh seekor hewan didefinisikan sebagai seluruh petak yang dilaluinya termasuk posisi awal hingga sesaat sebelum masuk kandang, yakni ayam diakhiri dengan petak (1, 1) dan bebek diakhiri dengan petak (2, 1).
Karena ayam dan bebek Pak Dengklek belum akur, apabila ada petak yang pernah dilalui oleh setidaknya seekor ayam dan setidaknya seekor bebek, maka akan terjadi perselisihan.
Sebagai contoh, berikut ini adalah ilustrasi kepulangan hewan yang tidak mengakibatkan perselisihan.
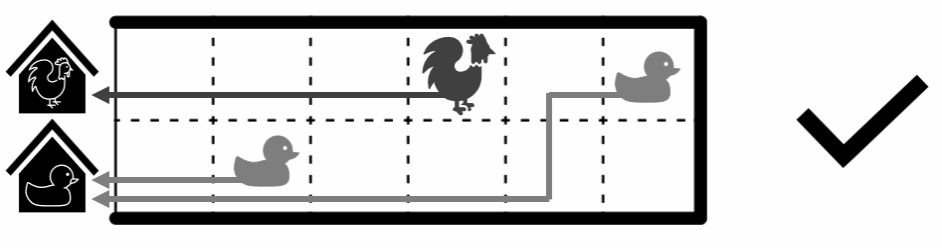
Sedangkan berikut ini adalah ilustrasi kepulangan hewan yang mengakibatkan perselisihan karena terdapat 3 petak yang pernah dilalui oleh setidaknya seekor ayam dan setidaknya seekor bebek.
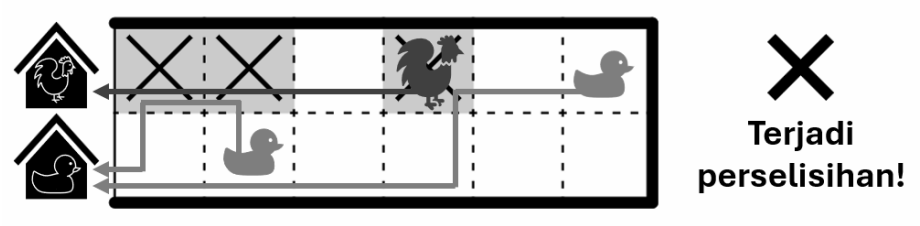
Setiap hewan memiliki nilai kerisihan yang didefinisikan sebagai jumlahan nilai-nilai kebecekan pada seluruh petak yang dilalui oleh rute hewan tersebut. Berapakah total nilai kerisihan paling kecil yang mungkin untuk seluruh hewan pulang ke kandang dengan syarat tidak terjadi perselisihan?
22.
Jawab →Asumsikan pekarangan Pak Dengklek berukuran 2 baris dan 1000 kolom. Diketahui juga bahwa hanya terdapat tepat 1 ekor ayam dan tepat 1 ekor bebek. Apabila pada petak (2, 500) terdapat seekor ayam, maka ada berapa banyak posisi awal bebek yang mungkin tidak mengakibatkan perselisihan ketika kedua hewan pulang ke kandang?
Tuliskan jawaban dalam bentuk ANGKA.
23.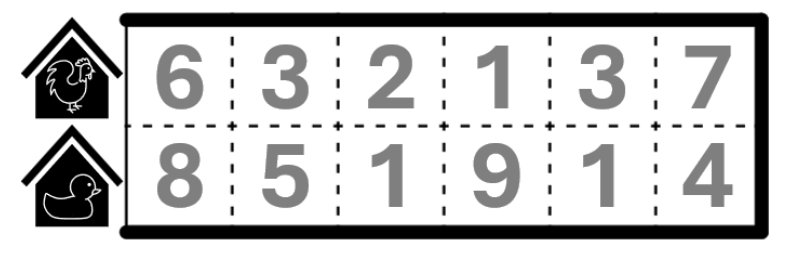
Jawab →Asumsikan pekarangan Pak Dengklek berukuran 2 baris dan 6 kolom. Diketahui pula bahwa kondisi lahan pekarangan direpresentasikan dengan matriks M berikut:

Apabila terdapat seekor ayam pada pekarangan tersebut di petak (1, 1) lalu juga ada 4 ekor bebek yang memenuhi kolom 5 hingga 6, atau dengan kata lain berada di petak (1, 5), (1, 6), (2, 5), dan (2, 6); maka berapakah total nilai kerisihan paling kecil yang mungkin untuk kelima hewan pulang ke kandang dengan syarat tidak terjadi perselisihan?
Tuliskan jawaban dalam bentuk ANGKA.
24.
KANDANG AYAM KANDANG BEBEK
Tulislah sebuah program dengan bahasa C++ sesuai deskripsi cerita dengan format dan batasan sebagai berikut. Perhatikan bahwa untuk setiap kasus uji berlaku time limit selama 3 detik dan memory limit sebanyak 256 MB.
Format Masukan:
Masukan diberikan dalam format berikut:
N
S_1
S_2
M_1,1 M_1,2 ... M_1,N
M_2,1 M_2,2 ... M_2,NFormat Keluaran:
Keluarkan sebuah baris berisi sebuah bilangan bulat yang menyatakan total nilai kerisihan paling kecil yang mungkin untuk seluruh hewan pulang ke kandang dengan syarat tidak terjadi perselisihan. Jika ternyata pasti terjadi perselisihan, keluarkan -1.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
6 A..... .B.... 6 3 2 1 3 7 8 5 1 9 1 4 | 19 |
6 A..... .B..B. 6 3 2 1 3 7 8 5 1 9 1 4 | 40 |
6 .A.A... .B..B. 6 3 2 1 3 7 8 5 1 9 1 4 | 54 |
6 A.A... .A..B. 6 3 2 1 3 7 8 5 1 9 1 4 | -1 |
Penjelasan Contoh
Pada contoh pertama, ayam dapat pulang ke kandang dengan hanya bergerak ke kiri sehingga rute yang dilaluinya hanyalah melewati petak (1, 1) dengan nilai kerisihan 6. Untuk bebek, ia dapat pulang ke kandang dengan bergerak ke kiri dua kali sehingga rute yang dilaluinya adalah melewati petak (2, 2) dan (2, 1) dengan nilai kerisihan 5 + 8 = 13. Total nilai kerisihan dari seluruh hewan adalah 6 + 13 = 19.
Pada contoh kedua, terdapat seekor bebek tambahan dari contoh pertama. Untuk mendapatkan kerisihan terkecil, bebek tambahan ini secara berturut-turut akan bergerak ke atas, kiri, kiri, bawah, kiri, dan kiri untuk pulang ke kandang. Dapat dihitung bahwa nilai kerisihan bebek tersebut adalah 1 + 3 + 1 + 2 + 1 + 5 + 8 = 21, sehingga total nilai kerisihan dari seluruh hewan menjadi 40.
Pada contoh ketiga, dapat dibuktikan bahwa total nilai kerisihan paling kecil adalah 54 dengan seluruh hewan hanya bergerak ke kiri saja. Perhatikan bahwa rute yang dilalui bebek pada petak (2, 5) tidak sama dengan yang ada pada contoh kedua karena dapat mengakibatkan perselisihan.
Pada contoh keempat, perhatikan bahwa rute yang dilalui bebek pasti akan pernah bersilangan dengan rute ayam sehingga terjadi perselisihan.
Batasan
- 1 ≤ N ≤ 100 000
- S1 dan S2 masing-masing memiliki panjang N dan hanya terdiri dari karakter ‘A’, ‘B’, dan ‘.’
- Dijamin bahwa terdapat setidaknya 1 ayam dan setidaknya 1 bebek di pekarangan
- 1 ≤ Mi,j ≤ 1 000 000
Batasan Tambahan untuk Subsoal 1 (Mudah)
- Dijamin bahwa banyaknya ayam adalah tepat 1, dan ayam tersebut berada pada petak (1, 1)
Batasan Tambahan untuk Subsoal 2 (Sulit)
Tidak ada batasan tambahan pada subsoal ini.
Peringatan
Untuk dapat menjawab pertanyaan ini dengan benar, Anda mungkin perlu menggunakan tipe data long long untuk dapat menyimpan data dengan nilai yang besar. Tipe data int saja mungkin tidak cukup!