Olimpiade Sains Provinsi (OSP) 2022 - Komputer
1.
Jawab →Pada sebuah toko buah diketahui informasi sebagai berikut:
| Buah | Jumlah Kalori Per Buah | Harga Per Buah | Stok Buah |
|---|---|---|---|
| Apel | 91 cal | Rp. 2.360 | 3 |
| Jeruk | 71 cal | Rp. 2.120 | 3 |
| Pisang | 105 cal | Rp. 1.890 | 5 |
| Kiwi | 103 cal | Rp. 3.770 | 10 |
| Mangga | 96 cal | Rp. 2.870 | 5 |
Pak Blangkon hanya memiliki uang Rp. 25.000, dan dia ingin membeli masing-masing buah maksimal sebanyak stok yang ada. Berapa jumlah maksimal kalori yang bisa didapatkan oleh Pak Blangkon? {tuliskan jawaban dalam bentuk ANGKA saja}
2.
Jawab →Kwak, Kwik, Kwuk, Kwek, Kwok ditugasi sebagai seorang diplomat. Kwak hanya dapat berbicara bahasa Inggris dan Jerman. Kwik hanya berbicara dalam bahasa Perancis, Jepang, dan Cina. Kwuk hanya dapat berbicara bahasa Jerman. Kwek hanya berbicara dalam bahasa Inggris, Jepang, dan Cina. Kwok hanya dapat berbicara dalam bahasa Perancis dan Jerman.
Ada berapa banyak pasangan diplomat yang harus menggunakan penterjemah dalam berkomunikasi? {tuliskan jawaban dalam bentuk ANGKA saja}
3.
Jawab →Kwak menuliskan kata "INFORMATIC" pada kertas berulang kali tanpa dipisahkan spasi. Huruf apa yang ditulis oleh Kwak pada urutan ke-22022 dan ke-32023? {tuliskan jawaban dalam bentuk DUA HURUF KAPITAL tanpa spasi}
4.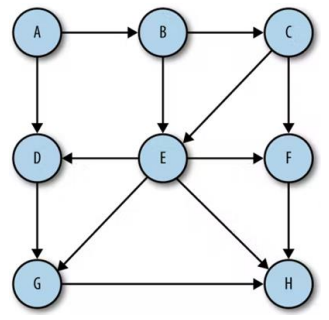
Jawab →Pak Dengklek memiliki pekarangan yang berisi 8 kandang yang diberi label A, B, C, D, E, F, G dan H sebagai berikut:

Tanda panah antara dua kandang (X, Y) menandakan bahwa terdapat jalan setapak yang bisa dilalui dari kandang X ke kandang Y namun tidak sebaliknya. Jika saat ini posisi Pak Dengklek ada di kandang A, dan ingin menuju ke kandang H. Ada berapa rute yang bisa dilalui Pak Dengklek dari kandang A ke kandang H, di mana setiap kandang dapat dikunjungi maksimal satu kali? {tuliskan jawaban dalam bentuk ANGKA saja}
5.
Jawab →Bebek-bebek Pak Dengklek akan mengikuti Olimpiade Sains Nasional Bebek. Sebelum bertanding setiap bebek harus mengikuti 8 jenis latihan, yaitu F, G, H, J, K, L, M dan N. Setiap latihan harus diambil tepat satu kali secara berurutan setiap harinya. Jadwal latihan tersebut dibatasi oleh hal-hal berikut:
- Latihan N selalu diambil di hari pertama
- Latihan F selalu diambil tepat setelah latihan G diambil
- Latihan F hanya bisa diambil jika latihan H sudah diambil
- Latihan J dan M harus dipisahkan oleh dua hari yang berurutan.
Ada berapa banyak kemungkinan urutan latihan yang bisa diambil oleh bebek-bebek Pak Dengklek? {tuliskan jawaban dalam bentuk ANGKA saja}
6.
Jawab →Pak Dengklek berencana memasang tiang untuk bebek-bebeknya bermain pada lahan berbentuk persegi panjang. Panjang dan lebar lahan tersebut belum ditentukan, namun kelilingnya harus 100 m. Pada lahan tersebut nantinya akan dikelilingi tembok. Jarak antara tiang harus sebesar minimal 2 meter. Selain itu, jarak antar tiang dengan tembok juga harus sebesar minimal 2 meter. Jika dilihat dari atas, tiang akan seperti titik pada koordinat dua dimensi. Berapa banyak tiang maksimal yang bisa dibuat oleh Pak Dengklek pada lahan tersebut? {tuliskan jawaban dalam bentuk ANGKA saja}
7.
Jawab →Pak Dengklek akan membentuk sebuah tim yang akan bertanding pada Olimpiade Olahraga Bebek pada cabang Bola Voli. Tim yang dibentuk harus terdiri dari 3 ekor bebek jantan dan 3 ekor bebek betina, yang dipilih dari 6 ekor bebek jantan dengan berat berbeda dan 6 ekor bebek betina dengan berat yang berbeda juga. Dari pengalaman sebelumnya diketahui bahwa semakin berat seekor bebek, maka semakin kuat dalam bertanding. Oleh sebab itu dalam tim yang dibentuk tersebut, Pak Dengklek ingin memastikan bahwa tim hanya boleh mencakup paling banyak satu anggota dengan berat badan paling ringan dari kedua jenis kelamin bebek. Dengan kata lain, bebek jantan paling ringan dan bebek betina paling ringan tidak boleh dipilih sekaligus. Berapa banyak cara untuk menyusun tim tersebut? {tuliskan jawaban dalam bentuk ANGKA saja}
8.
Jawab →Pak Dengklek ditunjuk menjadi ketua panitia Konser Musik Bebek. Konser akan dilaksanakan pada sebuah gedung pertunjukan berbentuk sektor lingkaran yang terdiri dari 6 baris kursi penonton. Pada baris pertama (baris paling depan) terdiri dari 25 kursi penonton, baris kedua terdiri dari 35 kursi penonton, baris ketiga terdiri dari 50 kursi penonton, baris keempat terdiri dari 70 kursi penonton, baris kelima terdiri 95 kursi penonton, dan baris keenam terdiri dari 125 kursi penonton. Diketahui bahwa harga tiket pada kursi baris paling depan adalah paling mahal dan selisih harga tiket antara dua baris yang berdekatan adalah Rp. 10.000. Jika diasumsikan semua kursi penonton penuh dan Pak Dengklek menginginkan agar diperoleh pemasukan Rp. 22.500.000, berapakah harga tiket pada baris ketiga? {tuliskan jawaban dalam bentuk ANGKA saja, sebagai contoh jika jawaban anda adalah Rp. 30.000 maka cukup tulis jawaban 30000}
9.
Jawab →Kwok sangat menyukai permen dan menyimpan permennya di dalam kotak yang dia miliki. Diketahui bahwa setiap tiga hari sekali, dia pasti akan memakan sebanyak 3 permen atau sebanyak sisa permen yang ada jika jumlahnya kurang dari 3. Setiap satu minggu sekali Pak Dengklek akan membelikan Kwok sebanyak 5 permen baru. Pak Dengklek membelikan permen di pagi hari, dan Kwok selalu makan permen di malam hari sebelum tidur. Jika pada hari ke-1 jumlah permen Kwok ada sebanyak 100 buah, Kwok pertama kali makan permen pada hari ke-3 dan Pak Dengklek pertama kali membelikan permen untuk Kwok pada hari ke-7, pada hari ke berapa paling cepat permen Kwok akan habis? {tuliskan jawaban dalam bentuk ANGKA saja}
10.
Jawab →Kwak, Kwik, Kwuk, Kwek dan Kwok masing-masing tinggal di satu kandang berbeda. Kandang Kwuk ada di sebelah utara kandang Kwak. Kandang Kwik bersebelahan dengan kandang Kwak. Kandang kwok terletak paling selatan. Kandang Kwek ada di sebelah tenggara kandang Kwuk. Kandang siapa yang berada di tengah-tengah? {tuliskan jawaban dalam huruf kecil semua}
Deskripsi Untuk Soal Nomor 11 dan 14
B1. Lampu Hias
DESKRIPSI CERITA
Pak Dengklek memiliki tiga lampu hias. Setiap lampu akan menyala setiap rentang waktu tertentu selama satu detik kemudian mati lagi. Lampu pertama menyala setiap rentang waktu P detik, lampu kedua menyala setiap rentang waktu Q detik, sedangkan lampu ketiga menyala setiap rentang waktu R detik. Di awal, ketiga lampu tersebut menyala secara bersamaan. Pak Dengklek bertanya-tanya, kapan lagi ketiga lampu tersebut akan menyala bersamaan?
11.
Jawab →Jika diketahui P = 4, Q = 10, dan R = 12, apakah ketiga lampu akan menyala bersamaan pada detik ke 3000?
Jawaban: ............... {tuliskan jawaban dalam bentuk YA/TIDAK}
12.
Jawab →Jika diketahui P = 1, Q = 2, dan R = 3, kapankah waktu terdekat berikutnya dimana ketiga lampu akan menyala lagi secara bersamaan?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
13.
Jawab →Jika diketahui P = 4, Q = 6, dan R = 9, kapankah waktu terdekat berikutnya dimana ketiga lampu akan menyala lagi secara bersamaan?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
14.
Jawab →LAMPU HIAS
Buatlah program menggunakan bahasa C/C++ sesuai deskripsi cerita di atas untuk menentukan minimal pengantaran dengan ketentuan sebagai berikut:
Format Masukan:
Baris pertama berisi sebuah tiga buah bilangan P, Q, R. Baris berikutnya berisi sebuah bilangan bulat positif N, menyatakan banyaknya pertanyaan Pak Dengklek. N buah baris berikutnya berisi masing-masing sebuah bilangan bulat positif T, menyatakan waktu dalam detik setelah ketiga lampu dinyalakan.
Format Keluaran:
N buah baris yang masing-masing berisi string berisi teks YA atau TIDAK (dalam huruf besar) yang menyatakan apakah pada waktu T tersebut, ketiga lampu menyala bersamaan atau tidak.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
4 6 9 4 10 36 90 100 | TIDAK YA TIDAK TIDAK |
Penjelasan Contoh:
Pada kasus ini, lampu pertama akan menyala setiap 4 detik, lampu kedua setiap 6 detik, dan lampu ketiga setiap 9 detik. Pada awalnya (T=0) semua lampu menyala bersamaan. Pada detik ke-36, ketiga lampu akan menyala lagi secara bersamaan. Namun pada detik ke-10, ke-90 dan ke-100, ketiga lampu tidak semuanya menyala secara bersamaan.
Batasan:
Untuk semua kasus uji berlaku:
- 1 ≤ P, Q, R ≤ 109
- 1 ≤ N ≤ 100 000
- 1 ≤ T ≤ 1018
Untuk 50% kasus uji berlaku:
- 1 ≤ N ≤ 100
- 1 ≤ P, Q, R ≤ 1000
- 1 ≤ T ≤ 109
Deskripsi Untuk Soal Nomor 15 dan 18
B2. Mengangkut Bebek
DESKRIPSI CERITA
Pak Dengklek sedang mengumpulkan bebek-bebeknya untuk diangkut ke tempat penangkaran bebek yang baru dibangun. Untuk mengangkut bebek-bebek tersebut, Pak Dengklek akan memesan kandang-kandang dari jasa pengangkut bebek. Setiap kandang bebek memiliki kapasitas (yaitu banyaknya bebek yang mampu ditampung di dalam kandang tersebut) serta memiliki biaya angkut yang dinyatakan dalam satuan rupiah per kg berat bebek. Misalkan ada K buah kandang, maka kita memiliki besaran-besaran P1, …, PK yang menyatakan kapasitas masing-masing kandang, serta C1, …, CK yang menyatakan biaya angkut per kg berat bebek dari masing-masing kandang.
Untuk meminimalkan biaya pengangkutan bebek, Pak Dengklek pertama-tama melakukan pendataan berat semua bebek-bebeknya. Kita dapat mengasumsikan berat semua bebek dapat dinyatakan sebagai bilangan bulat positif. Dari hasil pengukuran bobot N ekor bebek, Pak Dengklek mendapatkan besaran-besaran B1, …, BN yang menyatakan besarnya berat masing-masing bebek tersebut. Selanjutnya, Pak Dengklek harus mengatur bebek mana yang akan dimasukkan ke kandang yang mana agar didapatkan total biaya pengangkutan yang paling. Namun, sampai disini, sayangnya Pak Dengklek masih kebingungan, bagaimana strategi terbaik untuk melakukan hal ini. Dapatkah Anda membantu Pak Dengklek?
[Asumsikan bahwa total kapasitas kandang akan mencukupi untuk memasukkan semua bebek, atau dengan kata lain, P1 + … + PK ≥ N]
15.
Jawab →Jika Pak Dengklek akan mengangkut bebek-bebek dengan bobot B1 = 2, B2 = 2, dan B3 = 3 pada kandang dengan biaya angkut C1 = 5 rupiah per kg dan kapasitas P1 = 4, berapakah biaya pengangkutan yang harus dikeluarkan Pak Dengklek untuk satu kandang tersebut?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
16.
Jawab →Jika ada tiga kandang (K = 3) dengan kapasitas yang sama (P1 = P2 = P3 = 3) sedangkan biaya angkut dari masing-masing kandang adalah C1 = 5, C2 = 2 dan C3 = 3, sedangkan bebek Pak Dengklek ada 7 ekor (N = 7) dengan bobot yang kebetulan sama semua (B1 = … = B7 = 5), maka berapakah biaya terkecil yang perlu dibayarkan oleh Pak Dengklek untuk mengangkut semua bebek-bebeknya?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
17.
Jawab →Diketahui ada 3 buah kandang (K = 3) dengan kapasitas P1 = 6, P2 = 3, dan P3 = 4, dengan biaya angkut per kg berat bebek dari masing-masing kandang adalah C1 = 2, C2 = 1 dan C3 = 3 rupiah per kg. Jika diketahui bahwa Pak Dengklek memiliki 9 ekor bebek (N = 9) dengan berat masing masing (B1, …, B9) adalah 3, 2, 2, 4, 5, 3, 6, 8, dan 7, maka berapakah biaya angkut terkecil yang diperlukan oleh Pak Dengklek?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
18.
MENGANGKUT BEBEK
Buatlah program menggunakan bahasa C/C++ untuk membantu menjawab pertanyaan Pak Dengklek di atas.
Format Masukan:
Baris pertama berisi sebuah bilangan K, menyatakan banyaknya bilangan. 2 baris berikutnya berisi masing-masing K buah bilangan bulat positif, menyatakan nilai kapasitas setiap kandang (P1, …, PK) serta biaya angkut untuk setiap kandang dalam satuan rupiah per kg berat bebek (C1, …, CK).
Kemudian baris ketiga berisi sebuah bilangan bulat N, menyatakan banyaknya bebek Pak Dengklek. Baris keempat berisi N buah bilangan bulat positif, menyatakan berat bebek-bebek Pak Dengklek dalam satuan kilogram.
Format Keluaran:
Keluaran terdiri atas satu baris berisi sebuah bilangan bulat positif, menyatakan total biaya terkecil yang diperlukan oleh Pak Dengklek untuk mengangkut semua bebek-bebeknya menggunakan satu atau lebih kandang-kandang yang ada.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
2 3 4 5 2 6 4 1 5 2 3 2 | 43 |
Penjelasan Contoh:
Pak Dengklek dapat memasukkan bebek ke-2 dan 4 (dengan bobot 1 kg dan 2 kg) ke dalam kandang pertama (dengan kapasitas 3 dan biaya per kg = 5) sehingga biaya yang dibutuhkan untuk kandang pertama adalah (1 + 2) x 5 = 15. Kemudian Pak Dengklek memasukkan bebek sisanya (yaitu bebek ke-1, 3, 5, dan 6 (dengan bobot 4, 5, 3 dan 2 kg) ke kandang kedua (dengan kapasitas 4 dan biaya angkut 2 per kg) sehingga kandang kedua memerlukan biaya (4 + 5 + 3 + 2) x 2 = 28. Biaya total kedua kandang berarti adalah 15 + 28 = 43. Tidak ada cara pengangkutan bebek yang lain ke dalam kandang-kandang tersebut yang menyebabkan biaya angkut menjadi lebih kecil dari 43. Oleh karena itu, jawaban yang diinginkan adalah 43.
Batasan:
Untuk semua kasus uji berlaku:
- 1 ≤ K ≤ 1000
- 1 ≤ N ≤ 100 000
- Untuk setiap Bi berlaku 0 < Bi ≤ 106
- Untuk setiap Pi berlaku 0 < Pi ≤ 100 000
- Untuk setiap Ci berlaku 0 ≤ Ci ≤ 106
Untuk 50% kasus uji berlaku:
- B1 = B2 = … = BN (semua bebek memiliki berat yang sama).
Deskripsi Untuk Soal Nomor 19 dan 22
B3. Dewan Perwakilan Bebek
DESKRIPSI CERITA
Pak Dengklek akan membentuk dewan perwakilan bebek yang terdiri dari beberapa bebek yang diambil dari N kandidat bebek. Bebek ke-i mempunyai tingkat ego Ei. Dewan perwakilan bebek mempunyai tingkat perpecahan max(Ei) - min(Ei) yaitu selisih antara tingkat ego tertinggi dan terendah. Apabila tingkat perpecahan melebihi P maka dewan perwakilan bebek akan bubar. Pak Dengklek penasaran, apabila bebek ke-X harus menjadi anggota dewan perwakilan bebek, berapa anggota dewan perwakilan bebek maksimal yang dapat dibentuk agar tidak bubar? Pak Dengklek akan menanyakan pertanyaan tersebut sebanyak Q kali.
19.
Jawab →Diberikan tingkat ego bebek E = [1, 7, 4, 8, 10].
Apabila kandidat yang dipilih adalah bebek 2, 3, dan 4, berapa tingkat perpecahan yang terbentuk?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
20.
Jawab →Diberikan tingkat ego bebek E = [1, 7, 4, 8, 10].
Apabila ingin membentuk dewan perwakilan bebek yang terdiri dari 3 bebek, berapa tingkat perpecahan minimal yang dapat dicapai?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
21.
Jawab →Diberikan tingkat ego bebek E = [1, 7, 4, 8, 10].
Dengan P = 7, berapa banyak anggota dewan perwakilan bebek maksimal yang dapat dibentuk?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
22.
Jawab →DEWAN PERWAKILAN BEBEK
Buatlah program menggunakan bahasa C/C++ untuk menghitung banyak anggota dewan perwakilan bebek maksimal dengan ketentuan sebagai berikut:
Format Masukan:
Baris pertama berisi dua buah bilangan N, P, dan Q. Baris kedua berisi N buah bilangan Ei yang menyatakan tingkat ego dari masing-masing bebek.
Q baris berikutnya berisi bilangan X.
Format Keluaran:
Q buah baris berisi jawaban dari pertanyaan Pak Dengklek.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
6 5 2 1 6 8 3 10 2 2 5 | 4 3 |
Penjelasan Contoh:
Pada pertanyaan pertama, Pak Dengklek memilih bebek 1, 2, 4, dan 6. Pada pertanyaan kedua, Pak Dengklek memilih bebek 2, 3, dan 5.
Batasan:
Untuk kasus uji berlaku:
- 1 ≤ Q ≤ N ≤ 100 000
- 0 ≤ P, Ei ≤ 109
- 1 ≤ X ≤ N
Untuk 50% kasus uji berlaku:
- Q = 1
Deskripsi Untuk Soal Nomor 23 dan 26
B4. Memasang Karpet
DESKRIPSI CERITA
Untuk membantu menyeberangkan bebek-bebeknya, Pak Dengklek ingin membuat sebuah jembatan dengan panjang M meter dan lebar N meter. Pak Dengklek mempunyai 2 jenis karpet dengan bentuk seperti pada gambar di bawah.
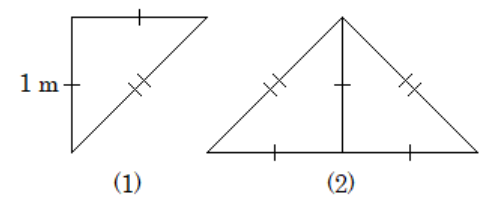
Karpet-karpet tersebut dapat dirotasi 90°, 180°, 270°, maupun tidak dirotasi sama sekali. Pak Dengklek penasaran, berapa banyak cara memasang karpet untuk menutupi seluruh jembatan sehingga tidak ada karpet yang tumpang tindih maupun keluar jembatan? Karena jawaban bisa jadi sangat besar, Pak Dengklek hanya penasaran hasilnya dalam modulo 1 000 000 007.
23.
Jawab →Jika N = 2, M = 5 dan hanya boleh menggunakan karpet jenis 1, berapa banyak cara menutup jembatan?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
24.
Jawab →Jika N = 1, M = 5, berapa banyak cara menutup jembatan?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
25.
Jawab →Jika N = 2, M = 3, berapa banyak cara menutup jembatan?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
26.
Jawab →MEMASANG KARPET
Buatlah program menggunakan bahasa C/C++ untuk menentukan nomor kartu pertama Pak Dengklek dengan ketentuan sebagai berikut:
Format Masukan:
Sebuah baris berisi dua buah bilangan N dan M yang menyatakan lebar dan panjang jembatan.
Format Keluaran:
Sebuah baris berisi sebuah bilangan yang menyatakan banyak cara memasang karpet dalam modulo 1 000 000 007.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
2 4 | 8568 |
1 2 | 6 |
Penjelasan Contoh:
Pada contoh kedua, jika Pak Dengklek tidak menggunakan karpet jenis 2 maka terdapat 4 cara. Jika Pak Dengklek menggunakan karpet jenis 2 maka terdapat 2 cara. Dengan demikian, totalnya terdapat 6 cara.
Batasan:
Untuk kasus uji berlaku:
- 1 ≤ N ≤ 2
- 1 ≤ M ≤ 100 000
Untuk 50% kasus uji berlaku:
- N = 1
Deskripsi Untuk Soal Nomor 27 dan 30
B5. Melompati Lapangan
DESKRIPSI CERITA
Pak Dengklek mempunyai lapangan yang terdiri dari N baris dan M kolom petak-petak persegi. Barisnya dinomori dari 1 sampai N, sedangkan kolomnya dinomori dari 1 sampai M. Petak yang berada di baris ke-i dan kolom ke-j dinotasikan dengan (i, j) dan mempunyai nilai A[i][j] (untuk semua 1 ≤ i ≤ N, 1 ≤ j ≤ M). Pak Dengklek dapat melompat dari (i, j) ke (i', j') jika dan hanya jika semua persyaratan berikut ini terpenuhi:
- i ≠ i' atau j ≠ j'
- i ≤ i' ≤ i + A[i][j]
- j ≤ j' ≤ j + A[i][j].
Jadi, jika A[i][j] = 0, maka Pak Dengklek tidak akan bisa melompat ke petak mana pun dari petak (i, j). Pak Dengklek bertanya-tanya, ada berapakah banyaknya urutan lompatan berbeda untuk bergerak dari (1, 1) ke (N, M). Dapatkah Anda membantu Pak Dengklek menjawab pertanyaan tersebut? Karena jawabannya bisa sangat besar, keluarkan jawabannya modulo 1 000 000 007.
27.
Jawab →Diketahui petak berukuran 3 x 4 dengan isi sebagai berikut:
| 3 | 1 | 0 | 4 |
| 2 | 0 | 0 | 1 |
| 4 | 1 | 3 | 2 |
Dapatkah Pak Dengklek bergerak dari petak (2, 4) ke petak (1, 2)?
Jawaban: ............... {tuliskan jawaban dalam bentuk YA/TIDAK}
28.
Jawab →Diketahui petak berukuran 3 x 4 dengan isi sebagai berikut:
| 3 | 1 | 0 | 4 |
| 2 | 0 | 0 | 1 |
| 4 | 1 | 3 | 2 |
Dapatkah Pak Dengklek bergerak dari petak (1, 2) ke petak (3, 4)?
Jawaban: ............... {tuliskan jawaban dalam bentuk YA/TIDAK}
29.
Jawab →Diketahui petak berukuran 3 x 4 dengan isi sebagai berikut:
| 3 | 1 | 0 | 4 |
| 2 | 0 | 0 | 1 |
| 4 | 1 | 3 | 2 |
Ada berapa banyak cara bagi Pak Dengklek untuk bergerak dari (1,1) ke (3, 4)?
Jawaban: ............... {tuliskan jawaban dalam bentuk ANGKA saja}
30.
Jawab →MELOMPATI LAPANGAN
Buatlah sebuah program dalam Bahasa C/C++ untuk menjawab pertanyaan Pak Dengklek sesuai dengan deskripsi pada cerita di atas!
Format Masukan:
Baris pertama berisi dua buah bilangan N dan M yang menyatakan ukuran petak yang dimiliki pak Dengklek (N = banyaknya baris, M = banyaknya kolom). N buah baris berikutnya masing-masing berisi M buah bilangan bulat non-negatif yang masing-masing terpisahkan dengan sebuah spasi. Setiap bilangan pada baris ke-i dan kolom ke-j menyatakan nilai A[i][j] (untuk semua 1 ≤ i ≤ N, 1 ≤ j ≤ M).
Format Keluaran:
Sebuah baris yang berisi sebuah bilangan K yang menyatakan banyaknya cara Pak Dengklek bergerak dari petak (1,1) ke petak (N, M) sesuai dengan aturan di atas, modulo 1 000 000 007.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|---|---|
2 3 2 0 1 1 1 3 | 4 |
Penjelasan Contoh:
Ada 4 urutan lompatan berbeda untuk bergerak dari (1, 1) ke (2, 3) pada contoh petak di atas, yaitu:
- (1, 1) → (1, 3) → (2, 3)
- (1, 1) → (2, 1) → (2, 2) → (2, 3)
- (1, 1) → (2, 2) → (2, 3)
- (1, 1) → (2, 3)
Batasan:
Untuk semua kasus uji berlaku:
- 1 ≤ N, M ≤ 2000
- 0 ≤ A[i][j] ≤ 2000
Untuk 50% kasus uji berlaku:
- 1 ≤ N, M ≤ 100