← Kembali ke Beranda

Olimpiade Sains Kota (OSK) 2025 - Komputer

1.

Pak Dengklek sedang bermain bersama bebek-bebeknya pada sebuah labirin. Setiap petak pada labirin bisa saja kosong (putih) atau berupa dinding (hitam).

Pak Dengklek dan bebek-bebeknya akan mulai pada petak di paling kiri atas (dengan label "M") dan akan selesai pada petak di paling kanan bawah (dengan simbol bintang). Mereka dapat bergerak dari suatu petak kosong ke petak kosong lain yang bersebelahan, dengan salah satu dari empat kemungkinan arah: atas (↑), kanan (→), bawah (↓), atau kiri (←). Untuk menyelesaikan labirin, Pak Dengklek dan bebek-bebeknya harus mengunjungi semua petak putih tepat satu kali.

Karena bebek-bebeknya merasa kesulitan untuk bermain labirin, Pak Dengklek akan membantu bebek-bebeknya dengan meletakkan tanda panah pada setiap petak kosong sedemikian sehingga apabila bebek-bebeknya mengikuti tanda panah, maka bebek-bebek Pak Dengklek dapat menyelesaikan sebuah labirin.

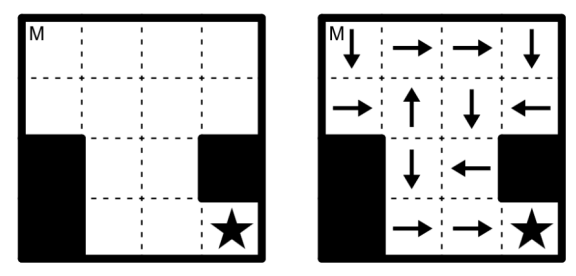
Gambar berikut mengilustrasikan peletakan tanda panah yang dilakukan oleh Pak Dengklek untuk menyelesaikan sebuah labirin berukuran 4×4 sesuai aturan tersebut.

Sekarang, Pak Dengklek akan menyelesaikan sebuah labirin berukuran 7×7 sebagai berikut.

Setelah seluruh tanda panah diletakkan, tanda panah apakah yang mungkin Pak Dengklek letakkan pada petak dengan tanda tanya?

Atas (↑)
Kanan (→)
Bawah (↓)
Kiri (←)
Ada lebih dari satu kemungkinan tanda panah

2.

Pak Dengklek membangun sebuah kandang yang memiliki 5 pintu dengan label A, B, C, D, dan E. Sebuah sensor dipasang di setiap pintu untuk menghitung banyaknya bebek yang keluar maupun yang masuk kandang melalui pintu tersebut.

Suatu hari, Pak Dengklek ingin menggunakan sensor tersebut untuk menghitung data keluar-masuk bebek dengan cara sebagai berikut:

Pada mulanya, seluruh bebek berada di dalam kandang.
Data perhitungan seluruh sensor dimulai dari 0.
Pak Dengklek membebaskan setiap bebek untuk berkeliaran keluar-masuk kandang melalui pintu mana pun.
Setelah beberapa waktu, Pak Dengklek menggiring seluruh bebek untuk masuk ke dalam kandang melalui pintu mana pun.

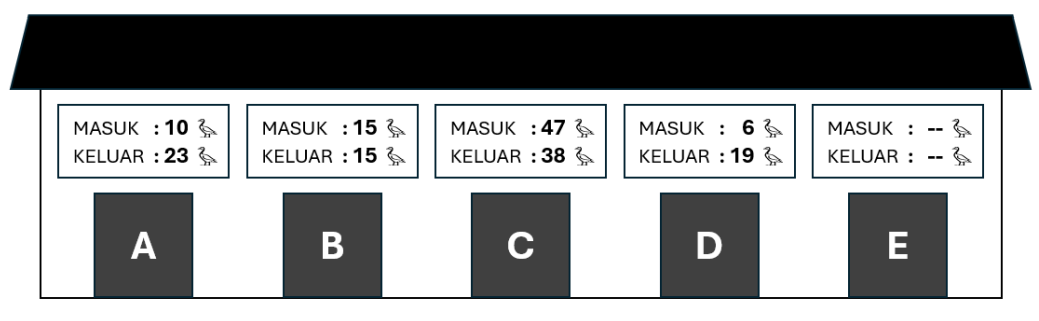
Sayangnya, saat ingin mengecek data bebek yang masuk dan keluar, Pak Dengklek baru menyadari bahwa sensor di pintu E rusak. Hanya terdapat informasi pada pintu A hingga D sebagai berikut.

Dari 5 pilihan berikut, manakah yang mungkin saja ditampilkan oleh sensor di pintu E?

MASUK: 18, KELUAR: 35
MASUK: 17, KELUAR: 17
MASUK: 0, KELUAR: 24
MASUK: 49, KELUAR: 32
MASUK: 36, KELUAR: 5

Lihat 1 jawaban →

3.

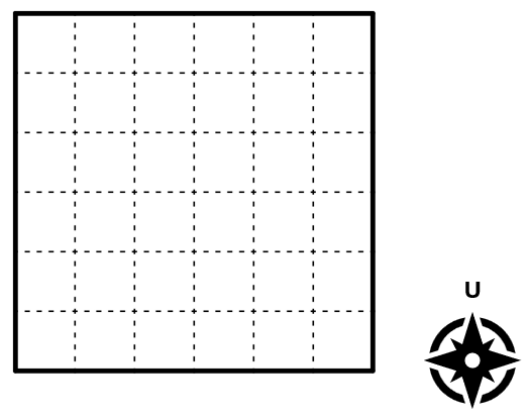
Kwak dan Kwik sedang bermain di sebuah pekarangan berbentuk petak dengan ukuran 6x6 yang dikelilingi oleh sebuah pagar.

Pada awalnya, Kwak akan memilih sebuah petak sebagai posisi awal. Kwak akan mulai pada petak tersebut dengan menghadap ke arah Utara (U). Selanjutnya, Kwik akan mengomando Kwak untuk melakukan seluruh instruksi pergerakan secara berturut-turut sebagai berikut:

Maju satu petak
Putar badan hadap kiri
Maju satu petak
Putar badan hadap kanan
Maju satu petak

Kwak akan menjalankan komando Kwik di atas sebanyak 2 kali secara berturut-turut tanpa jeda. Berapakah banyak kemungkinan posisi awal Kwak sedemikian sehingga tidak ada satu pun instruksi yang menyebabkan Kwak keluar pekarangan?

Tuliskan jawaban dalam bentuk ANGKA.

4.

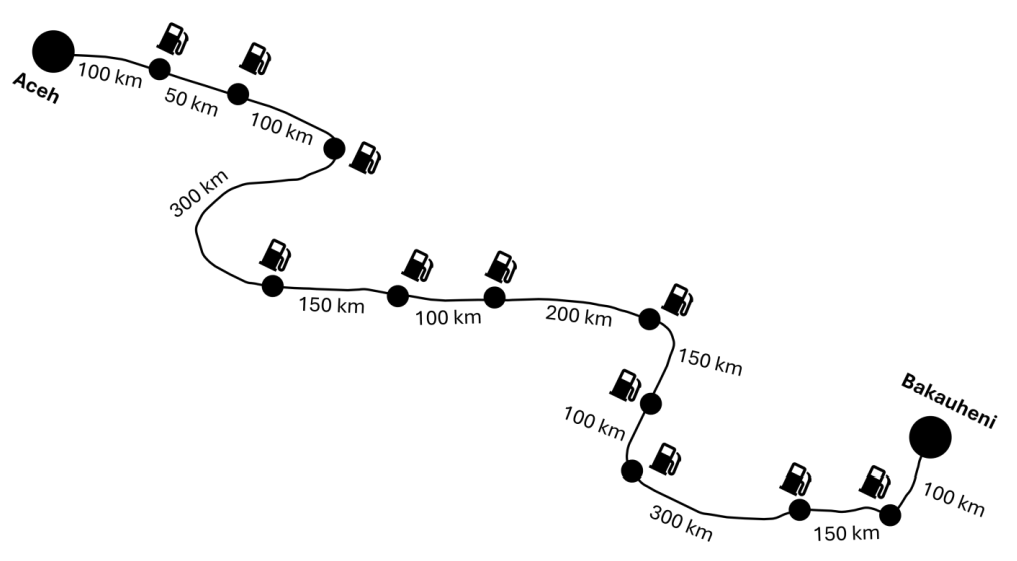
Pada lebaran tahun depan, Pak Dengklek berencana untuk pergi mudik dari Aceh ke Bakauheni menggunakan mobil. Karena jarak tempuh Aceh ke Bakauheni cukup jauh, maka Pak Dengklek perlu memperhatikan kapan ia harus mengisi bahan bakar mobilnya.

Pak Dengklek akan memulai perjalanannya di kota Aceh dengan tangki bahan bakar yang penuh. Apabila tangki bahan bakar mobil Pak Dengklek penuh, mobil Pak Dengklek dapat menempuh perjalanan hingga sejauh 500 km. Pak Dengklek dapat berhenti pada beberapa pom bensin yang tersedia (yang diberi label titik) untuk mengisi bahan bakar mobilnya hingga penuh kembali.

Berapa kalikah paling sedikit Pak Dengklek harus berhenti dan mengisi bahan bakar mobilnya untuk mencapai Bakauheni tanpa pernah kehabisan tangki bahan bakar?

Tuliskan jawaban dalam bentuk ANGKA.

5.

Bebek-bebek Pak Dengklek ingin bermain peran sebagai agen-agen detektif. Untuk menyamarkan identitas mereka, setiap bebek harus memiliki sebuah nama samaran yang unik.

Sebuah nama samaran yang valid haruslah memenuhi minimal satu dari dua aturan berikut:

Nama samaran dimulai dengan 0 hingga 2 karakter huruf ('A'-'Z'), lalu diikuti dengan 1 hingga 3 karakter digit ('0'-'9'). Contohnya yakni "BB007" atau "K3".
Nama samaran dimulai dengan 1 hingga 3 karakter digit ('0'-'9'), lalu diikuti dengan 0 hingga 2 karakter huruf ('A'-'Z'). Contohnya yakni "007BB" atau "47".

Apabila tidak boleh ada dua bebek yang memiliki nama samaran yang sama, maka berapakah banyak bebek paling banyak yang bisa bermain peran sebagai agen-agen detektif?

Tuliskan jawaban dalam bentuk ANGKA.

6.

Pak Dengklek dan 255 ekor bebeknya sedang bermain permainan "Pencarian Koin". Sebanyak 255 ekor bebek Pak Dengklek berbaris dari Barat ke Timur, dan masing-masing diberi nomor 1 hingga 255 secara berurutan dari paling Barat ke paling Timur.

Di awal permainan, para bebek berunding untuk menentukan siapa dari mereka yang akan memegang sebuah koin. Pak Dengklek tidak tahu bebek yang mana yang memegang koin, sedangkan semua bebek-bebek itu tentunya tahu siapa di antara mereka yang memegang koin. Pak Dengklek harus mencari bebek mana yang memegang koin.

Sekarang, aturan permainan adalah sebagai berikut:

Pak Dengklek akan bertanya ke salah satu di antara bebek-bebeknya.
Jika bebek yang ditanya tersebut memegang koin, permainan selesai.
Jika bebek tersebut tidak memegang koin, ia akan memberi tahu Pak Dengklek, apakah bebek yang memegang koin ada di sebelah Barat atau sebelah Timur dia.

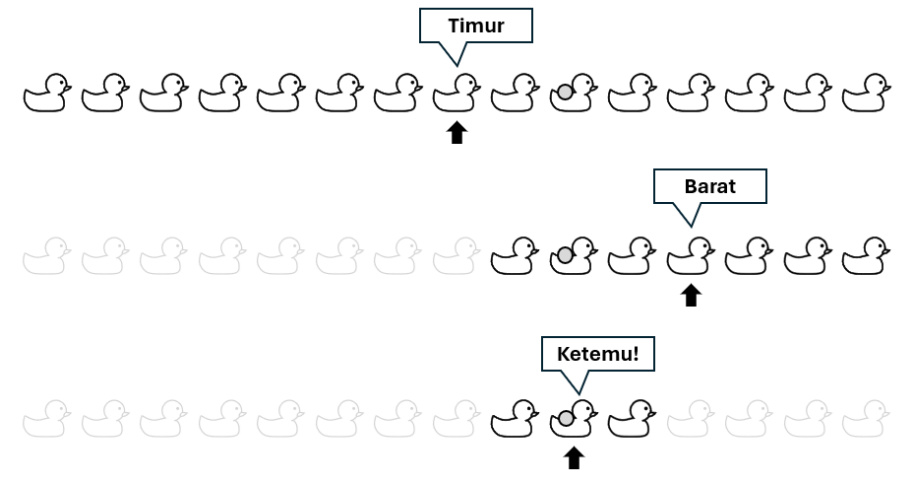
Untuk dapat menyelesaikan permainan secepat-cepatnya, Pak Dengklek akan menggunakan strategi sebagai berikut: ia akan selalu bertanya ke bebek yang posisinya di tengah-tengah barisan bebek yang masih mungkin berisi bebek yang memegang koin. Dijamin bahwa akan selalu ada sejumlah ganjil bebek yang masih mungkin menyimpan koin, sehingga dijamin terdapat satu bebek yang posisinya berada di tengah-tengah.

Dengan strategi tersebut, diketahui bahwa Pak Dengklek ternyata cukup bertanya ke 6 bebek sebelum menemukan siapa dari 255 ekor bebeknya yang memegang koin. Jawaban yang didapatkan Pak Dengklek secara berturut-turut adalah: "Barat", "Barat", "Timur", "Barat", "Timur", dan akhirnya koin ditemukan. Bebek nomor berapakah yang memegang koin?

Tuliskan jawaban dalam bentuk ANGKA.

7.

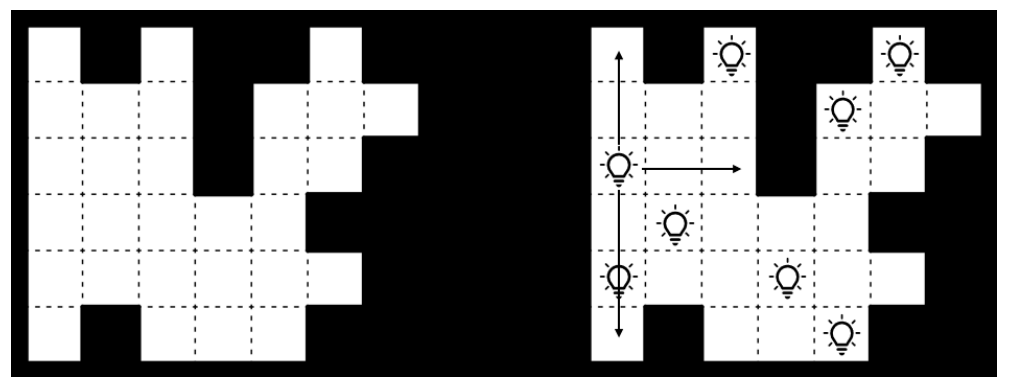
Pak Dengklek memiliki sebuah ruangan khusus di rumahnya sebagai tempat bermain bebek-bebeknya. Ruangan tersebut terdiri dari petak-petak putih yang dikelilingi oleh dinding berupa petak-petak hitam, dengan denah ruang yang diilustrasikan pada gambar di sebelah kiri.

Agar ruang bermain bebek-bebeknya tidak gelap, Pak Dengklek ingin memasang beberapa lampu pada beberapa petak putih. Apabila suatu petak dipasang oleh sebuah lampu, maka petak-petak yang terhubung berurutan tanpa terhalang oleh dinding apa pun secara vertikal (atas-bawah) maupun horizontal (kiri-kanan) dari petak tersebut akan terang. Pak Dengklek ingin seluruh petak putih terang.

Gambar di sebelah kanan mengilustrasikan salah satu kemungkinan pemasangan lampu oleh Pak Dengklek sehingga seluruh petak putih terang. Perhatikan juga ilustrasi penerangan salah satu lampu yang ditunjukkan oleh tanda panah.

Berapakah paling sedikit petak putih yang harus dipasang lampu oleh Pak Dengklek sehingga seluruh petak putih akan terang?

Tuliskan jawaban dalam bentuk ANGKA.

8.

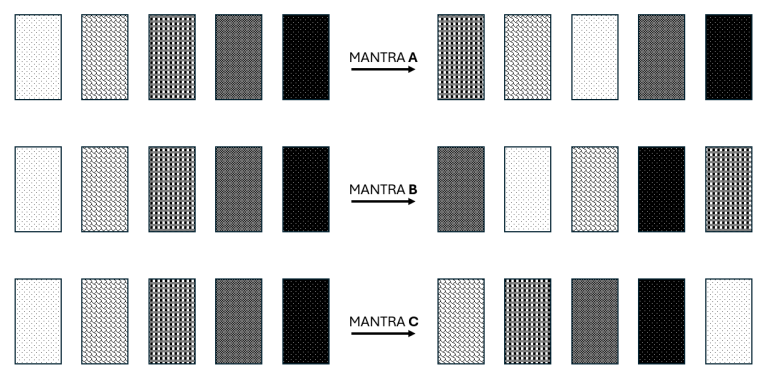
Kwek sedang bermain permainan kartu di komputer. Permainan ini melibatkan 5 buah kartu yang selalu tersusun dari kiri ke kanan. Dari paling kiri hingga paling kanan, kartu-kartu tersebut diberi label huruf v, w, x, y, dan z.

Ada beberapa mantra yang dapat diterapkan oleh Kwek untuk mengubah urutan kartu-kartu tersebut:

Mantra A: mengubah urutan kartu dari [v, w, x, y, z] menjadi [x, w, v, y, z]
Mantra B: mengubah urutan kartu dari [v, w, x, y, z] menjadi [y, v, w, z, x]
Mantra C: mengubah urutan kartu dari [v, w, x, y, z] menjadi [w, x, y, z, v]

Untuk memudahkan penerapan berbagai operasi mantra yang dapat dilakukan, Kwek menuliskan dengan notasi sebagai berikut:

P([i, j, k, l, m]) menunjukkan bahwa mantra P diterapkan pada urutan kartu [i, j, k, l, m].
Dua atau lebih mantra dapat juga dilakukan secara berurutan. Misalnya, PQ([i, j, k, l, m]) artinya mantra Q diterapkan pada urutan kartu [i, j, k, l, m], kemudian dilanjutkan dengan penerapan mantra P pada urutan kartu hasil mantra Q.
Serangkaian mantra dapat diulang dengan menggunakan mantra khusus F. Jika n adalah bilangan bulat positif, maka F(S, n) menunjukkan rangkaian mantra S yang diterapkan sebanyak n kali.

Apabila pada awalnya kartu [v, w, x, y, z] menyimpan angka [1, 2, 3, 4, 5], lalu Kwek akan menerapkan mantra dengan menuliskan:

F(BA, 2025)F(C, 2026)([v, w, x, y, z]),

maka bagaimanakah urutan angka yang disimpan oleh setiap kartu pada akhirnya?

[3, 2, 4, 5, 1]
[1, 3, 4, 5, 2]
[2, 4, 3, 5, 1]
[5, 4, 3, 1, 2]
[2, 3, 4, 5, 1]

9.

Setelah gagal lolos ke OSN Informatika tingkat nasional tahun lalu, Kwek berencana untuk ikut kembali di tahun ini. Sebagai persiapan, ia berencana untuk mengikuti serangkaian pelatihan. Setiap pelatihan memiliki nama, durasi (dalam hari), dan prasyarat berupa daftar pelatihan-pelatihan lain yang harus diselesaikan terlebih dahulu oleh Kwek agar dapat mengikuti pelatihan tersebut.

Dalam satu hari, Kwek boleh saja mengikuti lebih dari satu pelatihan. Namun, suatu pelatihan tidak bisa dipotong di tengah jalan. Tujuan Kwek adalah menyelesaikan seluruh pelatihan dalam waktu sesingkat-singkatnya.

Kode	Nama Pelatihan	Durasi (Hari)	Prasyarat
AA	Analisis Algoritma	3	CPP
BF	Brute-Force dan Strategi Pruning	6	AA & DS
CPP	Pemrograman Dasar C++	7	-
DNC	Divide-and-Conquer	1	DS
DP	Dynamic Programming	4	DNC
DS	Struktur Data	5	CPP
GRE	Greedy	2	BF & DP

Dengan informasi yang diberikan di atas, berapakah waktu paling minimum (dalam hari) yang dibutuhkan oleh Kwek untuk menyelesaikan seluruh pelatihan?

Tuliskan jawaban dalam bentuk ANGKA.

10.

Pak Dengklek bermimpi bahwa ia mendapatkan tujuh buah telur bebek yang diberi label dari 1 hingga 7. Diketahui bahwa tepat dua dari tujuh telur tersebut adalah telur emas. Sayangnya, secara kasat mata, semua telur tersebut terlihat sama di mata Pak Dengklek — jika mengabaikan nomor label telurnya. Oleh karena itu, Pak Dengklek menciptakan sebuah mesin pendeteksi telur emas.

Mesin pendeteksi telur emas ini akan bekerja sebagai berikut:

Pak Dengklek memasukkan beberapa (boleh satu atau lebih) telur ke dalam mesin untuk dicek.
Mesin akan melakukan pengecekan dan akan mengembalikan telur-telur yang dimasukkan tadi kembali ke Pak Dengklek.
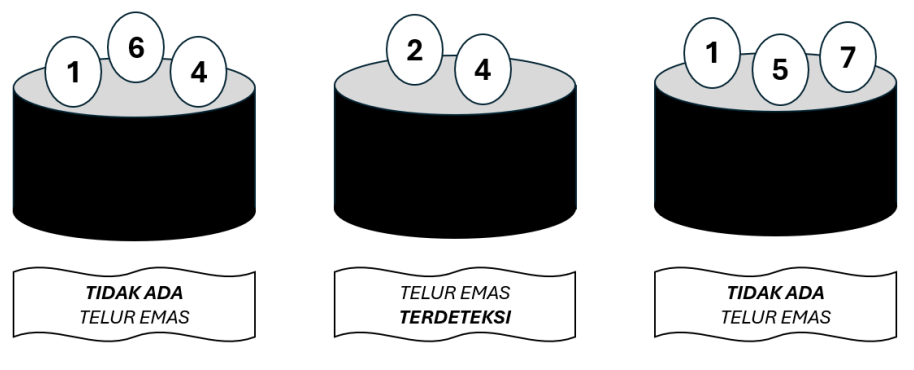
Mesin akan melaporkan hasil pengecekan yakni salah satu di antara dua kemungkinan berikut: "TIDAK ADA TELUR EMAS" yang artinya seluruh telur yang dimasukkan oleh Pak Dengklek tidak ada yang merupakan telur emas; atau "TELUR EMAS TERDETEKSI" yang artinya ada setidaknya satu telur emas yang dimasukkan oleh Pak Dengklek.

Perhatikan bahwa ketika mesin melaporkan "TELUR EMAS TERDETEKSI", tidak ada informasi tambahan yang dapat diketahui oleh Pak Dengklek, seperti telur yang mana yang merupakan telur emas. Pak Dengklek ingin menemukan kedua telur emas dari tujuh telur tersebut.

Sebagai contoh, berikut adalah ilustrasi mesin pendeteksi telur apabila telur 2 dan 3 adalah telur emas. Perhatikan bahwa ini adalah contoh, sehingga mungkin saja telur emas yang sesungguhnya merupakan pasangan telur yang lain.

Pak Dengklek ingin mencari sebuah strategi yang meminimumkan penggunaan mesin pendeteksi telur mau bagaimana pun pasangan telur emasnya. Dengan menggunakan strategi ini, dijamin bahwa Pak Dengklek dapat menentukan secara persis mana dua telur yang merupakan telur emas dengan menggunakan mesin pendeteksi telur emas paling banyak K kali. Berapakah nilai dari K?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 11 dan 13

Pak Dengklek memiliki sebuah mesin ajaib yang salah satu bagiannya berbentuk tabung dengan mekanisme buka tutup di atasnya. Selain itu, Pak Dengklek juga memiliki N buah koin yang dinomori dari 1 hingga N.

Mesin ajaib ini disebut juga sebagai Mesin BCS karena terdapat tiga tombol pada mesin tersebut:

Tombol B ("Buka"): Ketika ditekan, bagian atas tabung akan terbuka dan Pak Dengklek harus meletakkan koin dengan nomor terkecil miliknya yang belum pernah Pak Dengklek masukkan sebelumnya.
Tombol C ("Cetak"): Ketika ditekan, mesin akan mencetak nomor koin yang berada di bagian paling atas tabung ke selembar kertas, lalu secara otomatis mengeluarkan koin tersebut dari tabung. Perhatikan bahwa koin yang dikeluarkan ini tidak akan digunakan lagi oleh Pak Dengklek. Apabila tidak ada koin pada mesin BCS, maka penekanan tombol ini akan menghasilkan error.
Tombol S ("Stop"): Ketika ditekan, mesin akan memastikan bahwa tidak ada lagi koin di dalam tabung, lalu diakhiri dengan mengeluarkan kertas hasil cetakan yakni berupa nomor-nomor koin tanpa dipisahkan oleh spasi. Apabila masih ada koin pada mesin BCS, maka penekanan tombol ini akan menghasilkan error.

Karena Pak Dengklek ingin memasukkan seluruh N koin miliknya, dijamin bahwa Pak Dengklek akan melakukan tepat 2 × N + 1 penekanan tombol. Pak Dengklek juga menjamin bahwa urutan penekanan tombolnya tidak akan menghasilkan error.

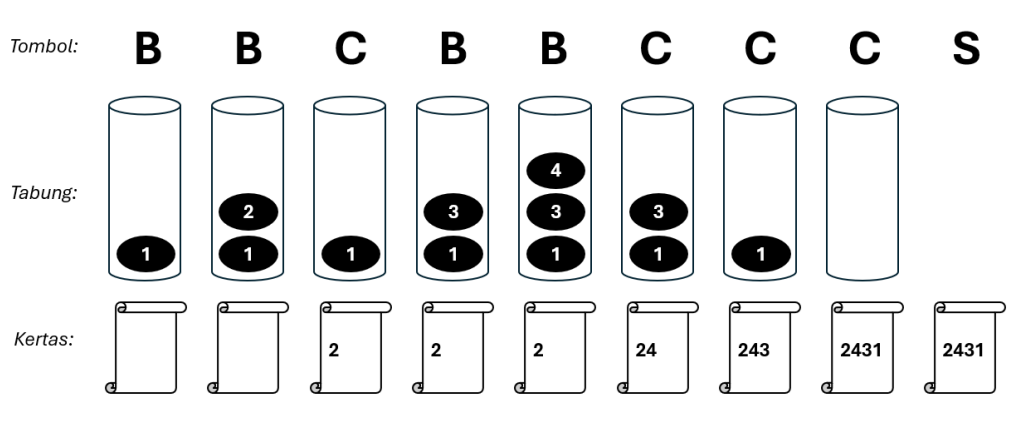
Sebagai contoh, Pak Dengklek memiliki N = 4 koin dan akan dilakukan penekanan tombol secara berurutan sebagai berikut: "BBCBBCCCS". Perhatikan bahwa kertas hasil cetakan pada akhirnya akan berisi "2431" dengan penjelasan sebagai berikut.

11.

Jika Pak Dengklek memiliki N = 6 koin dan melakukan penekanan tombol secara berurutan sebagai berikut: "BBCBCBBCCCBCS", maka apakah isi dari kertas hasil cetakan pada akhirnya?

Tuliskan jawaban dalam bentuk ANGKA tanpa tanda petik.

12.

Jika Pak Dengklek memiliki N = 9 koin dan setelah melakukan penekanan tombol didapatkan kertas hasil cetakan pada akhirnya berisi "543628971", maka bagaimanakah urutan penekanan tombol yang dilakukan oleh Pak Dengklek? Perhatikan bahwa urutan penekanan tombol harus diakhiri dengan tombol S ("Stop").

Tuliskan jawaban dalam bentuk STRING tanpa tanda petik.

13.

Jika Pak Dengklek memiliki N = 6 koin, dari 5 kemungkinan isi dari kertas hasil cetakan berikut, manakah yang sebenarnya tidak mungkin Pak Dengklek dapatkan?

"453216"
"321654"
"243651"
"534621"
"123456"

Deskripsi Untuk Soal Nomor 14 dan 16

Bebek-bebek Pak Dengklek baru saja menyelesaikan film petualangan "Perjalanan ke Barat". Karena mereka sangat menyukai film tersebut, hari ini mereka ingin sekali bertualang.

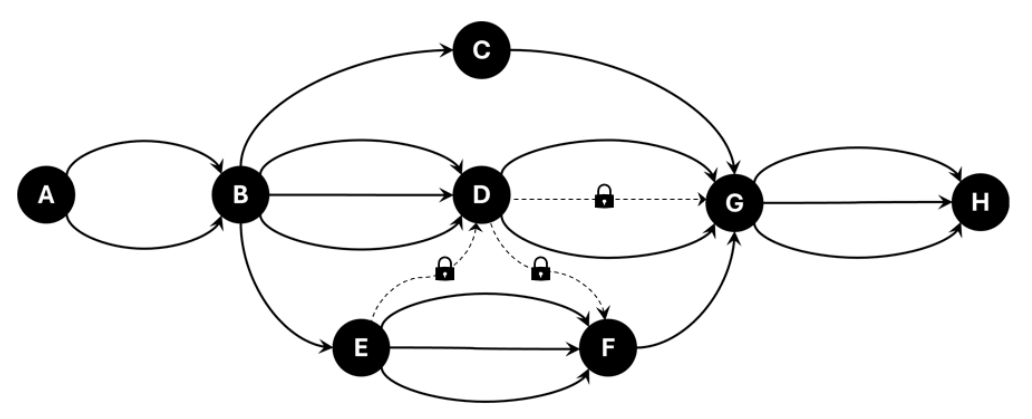
Petualangan mereka dinamakan "Perjalanan ke Timur", karena dari tempat mereka berasal yakni titik A, mereka hanya dapat bergerak ke arah kanan melewati lajur-lajur dengan arah panah. Mereka ingin mencapai titik terkanan yakni titik H. Namun, ternyata diketahui bahwa terdapat banyak sekali rute yang dapat mereka tempuh, misalnya dari titik A ke titik B saja ada 2 lajur berbeda yang dapat mereka lewati.

Setelah diteliti kembali, ternyata juga terdapat 3 lajur rahasia yang masing-masing ditutup dengan sebuah gembok, yakni lajur dari E ke D, dari D ke F, dan salah satu lajur dari D ke G. Untuk melewati lajur rahasia tersebut, dibutuhkan sebuah kunci sakti. Satu kunci hanya dapat digunakan untuk membuka gembok maksimal satu kali saja.

Bebek-bebek Pak Dengklek penasaran untuk menghitung banyaknya kemungkinan rute berbeda yang dapat mereka lalui jika mereka ingin pergi dari titik A ke titik H dengan syarat hanya boleh mengambil lajur ke arah kanan (mengikuti arah panah). Perhatikan bahwa dua kemungkinan rute dikatakan berbeda apabila ada lajur yang dilalui oleh satu rute tapi tidak dilalui oleh rute yang lainnya.

14.

Jika bebek-bebek Pak Dengklek tidak memiliki kunci sakti, berapakah banyak kemungkinan rute berbeda yang dapat mereka lalui?

Tuliskan jawaban dalam bentuk ANGKA.

15.

Jika bebek-bebek Pak Dengklek memiliki tiga kunci sakti, berapakah banyak kemungkinan rute berbeda yang dapat mereka lalui?

Tuliskan jawaban dalam bentuk ANGKA.

16.

Jika bebek-bebek Pak Dengklek memiliki hanya satu kunci sakti, berapakah banyak kemungkinan rute berbeda yang dapat mereka lalui?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 17 dan 19

Pak Dengklek menyukai estetika, sehingga ia ingin sekali membersihkan gudang di samping kandang-kandang bebeknya yang sudah lama tidak dirapikan.

Di dalam gudang tersebut ternyata ada banyak sekali kotak-kotak kardus penyimpanan. Setiap kotak kardus memiliki bentuk kubus. Agar lebih rapi, Pak Dengklek bisa saja menaruh sebuah kotak kardus di dalam sebuah kotak kardus lainnya, asalkan panjang sisi kotak kardus yang di dalam lebih kecil dibandingkan panjang sisi kotak kardus yang di luar. Perhatikan bahwa bisa jadi ada kotak kardus di dalam kotak kardus, yang berada di dalam kotak kardus, yang berada di dalam kotak kardus lainnya, dan seterusnya.

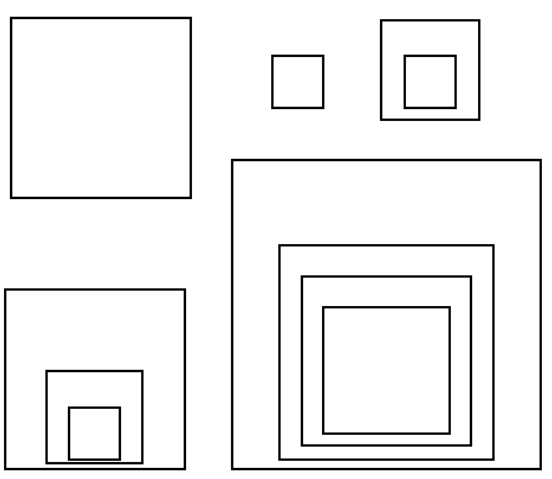
Karena alasan estetika, Pak Dengklek ingin agar seluruh kotak, jika dibuka, akan terlihat di dalamnya maksimal satu kotak kardus saja. Tentunya, jika memang terlihat satu kotak kardus di dalamnya, Pak Dengklek bisa saja membuka kotak kardus tersebut, dan di dalamnya juga harus terlihat maksimal satu kotak kardus saja, dan seterusnya.

Agar gudang terlihat lebih rapi, Pak Dengklek ingin meminimalkan banyaknya kotak kardus yang terlihat (dari luar) di gudang tersebut.

17.

Apabila terdapat 10 kotak kardus dengan panjang sisi masing-masing adalah:

1, 1, 2, 2, 2, 3, 3, 4, 6, 8;

maka berapakah banyaknya kotak kardus paling sedikit yang mungkin yang dapat terlihat dari luar?

Tuliskan jawaban dalam bentuk ANGKA.

18.

BENAR atau SALAH: Apabila seluruh kotak kardus di gudang memiliki panjang sisi yang berbeda-beda antara satu dengan yang lainnya, maka banyaknya kotak kardus paling sedikit yang mungkin yang dapat terlihat dari luar adalah satu kotak saja.

Tuliskan jawaban dalam bentuk BENAR/SALAH dengan huruf kapital.

19.

Terdapat 70 kotak kardus dengan daftar sebagai berikut.

Panjang Sisi	Banyaknya Kotak Kardus
2	5
3	12
5	19
8	4
13	15
21	7
34	8

Maka, berapakah banyaknya kotak kardus paling sedikit yang mungkin yang dapat terlihat dari luar?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 20 dan 22

Pak Dengklek memiliki 26 kartu ajaib. Pada awalnya, kartu ajaib pertama berisi huruf 'A', kartu ajaib kedua berisi huruf 'B', dan seterusnya hingga kartu ajaib ke-26 berisi huruf 'Z'.

Dengan menjentikkan jarinya satu kali, Pak Dengklek akan mengubah semua isi kartu ajaib miliknya sekaligus. Lebih detailnya, apabila kartu berisi suatu huruf, maka kartu tersebut akan berubah isinya menjadi suatu huruf lain, yang dapat disimak dalam tabel berikut.

Jika sebelumnya adalah	A	B	C	D	E	F	G	H	I	J	K	L	M
Maka akan berubah menjadi	B	C	B	C	F	H	F	I	F	E	E	N	L

Jika sebelumnya adalah	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
Maka akan berubah menjadi	M	P	T	P	Q	Q	U	V	W	X	T	W	V

20.

Pada awalnya, kartu ajaib pertama berisi huruf 'A', kartu ajaib kedua berisi huruf 'B', dan seterusnya hingga kartu ajaib ke-26 berisi huruf 'Z'. Apabila Pak Dengklek menjentikkan jarinya sebanyak 33 kali, maka apakah isi kartu ajaib ke-10 pada akhirnya?

Tuliskan jawaban dalam bentuk HURUF KAPITAL.

21.

Pada awalnya, kartu ajaib pertama berisi huruf 'A', kartu ajaib kedua berisi huruf 'B', dan seterusnya hingga kartu ajaib ke-26 berisi huruf 'Z'. Pak Dengklek menjentikkan jarinya sebanyak 3333 kali, lalu melihat isi seluruh kartu ajaib miliknya. Berapa banyak huruf berbeda yang dapat Pak Dengklek lihat pada kartu-kartu ajaib miliknya?

Tuliskan jawaban dalam bentuk ANGKA.

22.

Pada awalnya, kartu ajaib pertama berisi huruf 'A', kartu ajaib kedua berisi huruf 'B', dan seterusnya hingga kartu ajaib ke-26 berisi huruf 'Z'. Pak Dengklek menjentikkan jarinya sebanyak 333333 kali, lalu melihat isi seluruh kartu ajaib miliknya. Huruf apakah yang muncul paling banyak pada kartu-kartu ajaib milik Pak Dengklek? Jika terdapat lebih dari satu kemungkinan huruf, pilihlah huruf dengan indeks terkecil secara alfabetik.

Tuliskan jawaban dalam bentuk HURUF KAPITAL.

Deskripsi Untuk Soal Nomor 23 dan 25

Pak Dengklek memiliki N ekor bebek yang dinomori dari Bebek ke-1 hingga Bebek ke-N. Karena hari ini adalah Hari Mandi Nasional, Pak Dengklek ingin memandikan seluruh bebek-bebeknya.

Diketahui bahwa Pak Dengklek memiliki dua buah gayung. Dengan gayung pertama, Pak Dengklek dapat secara tepat mengambil X liter; sedangkan dengan gayung kedua, Pak Dengklek dapat secara tepat mengambil Y liter. Perhatikan bahwa Pak Dengklek tidak bisa mengira-ngira bagian dari gayung tersebut, sehingga Pak Dengklek tidak dapat mengambil tepat separuh dari X liter atau sepertiga dari Y liter misalnya.

Bebek-bebek Pak Dengklek sebenarnya tidak suka mandi. Sehingga, mereka memberikan dua persyaratan kepada Pak Dengklek agar mereka mau mandi sebagai berikut:

Sekali Pak Dengklek mengambil air dengan gayung, maka air tersebut harus langsung digunakan untuk mandi.
Bebek ke-P ingin mandi dengan air sebanyak tepat P liter.

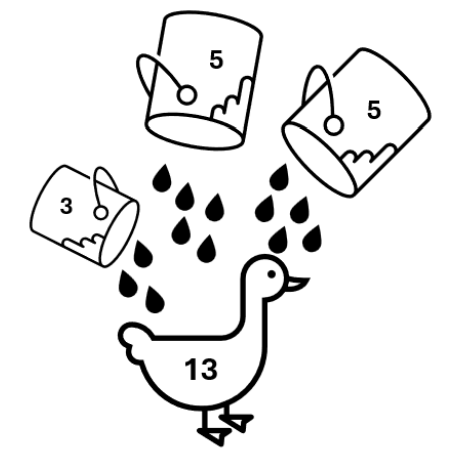
Sebagai contoh, dimisalkan Pak Dengklek memiliki dua gayung berukuran X = 3 liter dan Y = 5 liter. Dengan persyaratan-persyaratan yang telah disebutkan, untuk Bebek ke-13 misalnya, Pak Dengklek bisa memandikannya dengan mengambil air dari gayung 3 liter sebanyak sekali dan dari gayung 5 liter sebanyak dua kali. Namun, perhatikan bahwa Pak Dengklek tidak bisa memandikan beberapa bebek; misalnya Bebek ke-2 atau Bebek ke-4.

23.

Jika diketahui bahwa Pak Dengklek memiliki N = 20 bebek serta dua gayung berukuran X = 3 liter dan Y = 5 liter, maka berapakah banyak bebek yang tidak bisa dimandikan oleh Pak Dengklek?

Tuliskan jawaban dalam bentuk ANGKA.

24.

Jika diketahui bahwa Pak Dengklek memiliki N = 1000 bebek serta dua gayung berukuran X = 9 liter dan Y = 21 liter, maka berapakah banyak bebek yang tidak bisa dimandikan oleh Pak Dengklek?

Tuliskan jawaban dalam bentuk ANGKA.

25.

BENAR atau SALAH: Meskipun Pak Dengklek memiliki N = 1000000000000000000 bebek, hanya dengan dua gayung berukuran X = 3 liter dan Y = 100 liter saja, banyak bebek yang tidak bisa dimandikan oleh Pak Dengklek ternyata kurang dari 100 ekor.

Tuliskan jawaban dalam bentuk BENAR/SALAH dengan huruf kapital.

Deskripsi Untuk Soal Nomor 26 dan 28

Perhatikan potongan kode program berikut.

int TIGA(int N) {
    if (N <= 1) {
        return 1;
    } else if (N % 3 == 0) {
        return TIGA(N - 1) + TIGA(N - 3);
    } else if (N % 3 == 1) {
        return TIGA(N - 2);
    } else {
        return TIGA(N - 3);
    }
}

26.

Dari 5 pilihan pemanggilan berikut, manakah yang hasil kembaliannya paling besar?

TIGA(2)
TIGA(6)
TIGA(14)
TIGA(18)
TIGA(25)

27.

Berapa banyak dari 2025 pemanggilan TIGA(1), TIGA(2), TIGA(3), dan seterusnya hingga TIGA(2025); yang menghasilkan nilai kembalian berupa 1?

Tuliskan jawaban dalam bentuk ANGKA.

28.

Berapakah hasil dari penjumlahan:

TIGA(1) + TIGA(2) + TIGA(3) + ... + TIGA(100)?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 29 dan 31

Perhatikan potongan kode program berikut.

int GSI(vector<int> B, int x, int y) {
    return B[y] - B[x - 1];
}

int FUN(vector<int> A) {
    int N = A.size();

    vector<int> B;
    B.push_back(0);
    for (int i = 0; i < N; i++) {
        B.push_back(B[i] + A[i]);
    }

    int out = 0;
    for (int i = 1; i <= N; i++) {
        for (int j = i; j <= N; j++) {
            out = max(out, GSI(B, i, j));
        }
    }
    return out;
}

29.

Perhatikan bahwa pada pemanggilan fungsi FUN(A), akan terbentuk vector B di dalam fungsi tersebut. Apabila isi dari vector A adalah {1, 2, 3, 4, 5}, maka dari 5 pilihan berikut, manakah isi dari vector B?

{1, 3, 6, 10, 15}
{0, 1, 3, 6, 10, 15}
{0, 1, 2, 3, 4, 5}
{0, 2, 4, 6, 8, 10}
{15, 15, 15, 15, 15}

30.

Perhatikan bahwa pada pemanggilan fungsi FUN(A), akan terbentuk vector B di dalam fungsi tersebut. Apabila isi dari vector A adalah {1, 2, 3, 4, 5}, dari 5 pilihan pemanggilan berikut, manakah yang hasil kembaliannya paling besar?

GSI(B, 1, 4)
GSI(B, 2, 4)
GSI(B, 4, 5)
GSI(B, 5, 5)
GSI(B, 3, 4)

31.

Berapakah hasil kembalian dari pemanggilan:

FUN({3, -2, 4, -3, 1, -4, 2, -1, 4, 3, -2, 3, -4, 2, -2, 3})?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 32 dan 34

Perhatikan potongan kode program berikut.

int DUA(string S, string T) {
    int N = S.length();
    int M = T.length();

    int P = 0;
    for (int i = 0; i <= N - M; i++) {
        int Q = 1;
        for (int j = 0; j < M; j++) {
            if (S[i + j] != T[M - 1 - j]) {
                Q = 0;
            }
        }
        P += Q;
    }
    return P;
}

32.

Berapakah hasil kembalian dari pemanggilan:

DUA("ABCBAABCCBAABC", "CBA")?

Tuliskan jawaban dalam bentuk ANGKA.

33.

Akan dipanggil:

DUA("BBABAABBAAABBABBAAABBBAAABBABBA", T)

yang mana T adalah sebuah string dengan panjang minimal 3.

Dari seluruh kemungkinan nilai string T, berapakah hasil kembalian paling besar dari pemanggilan tersebut?

Tuliskan jawaban dalam bentuk ANGKA.

34.

Jika diketahui bahwa nilai string S = "ACCAAACCA", maka berapakah banyak kemungkinan string T sedemikian sehingga hasil kembalian dari pemanggilan DUA(S, T) sama dengan 2? Perhatikan bahwa tidak ada syarat mengenai panjang dari string T.

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 35 dan 37

Perhatikan potongan kode program berikut.

int RAHASIA(vector<int> A) {
    int N = A.size();

    int sum = 0;
    for (int i = 0; i < N; i++) {
        int ctr = 0;
        for (int j = 0; j < N; j++) {
            if (A[j] > A[i]) {
                ctr += 1;
            } else if (A[j] < A[i]) {
                ctr -= 1;
            }
        }
        if (ctr == 0) {
            sum += A[i];
        }
    }
    return sum;
}

int PETAK(vector<vector<int>> B) {
    int N = B.size();

    vector<int> C;
    for (int i = 0; i < N; i++) {
        C.push_back(RAHASIA(B[i]));
    }

    return RAHASIA(C);
}

35.

Berapakah hasil kembalian dari pemanggilan RAHASIA({16, 5, 20, 1, 11})?

Tuliskan jawaban dalam bentuk ANGKA.

36.

Berapakah hasil kembalian dari pemanggilan:

PETAK({16, 5, 20, 1, 11}, {2, 17, 13, 14, 19}, {15, 7, 21, 18, 9}, {25, 6, 4, 12, 22}, {23, 3, 24, 8, 10})?

Tuliskan jawaban dalam bentuk ANGKA.

37.

Akan dipanggil:

PETAK({a, b, c, d, e}, {f, g, h, i, j}, {k, l, m, n, o}, {p, q, r, s, t}, {u, v, w, x, y})

yang mana setiap huruf 'a' hingga 'y' akan berisi 25 bilangan bulat berbeda dari rentang 1 hingga 25.

Dari seluruh kemungkinan cara pengisian setiap hurufnya, berapakah hasil kembalian paling besar dari pemanggilan tersebut?

Tuliskan jawaban dalam bentuk ANGKA.

Deskripsi Untuk Soal Nomor 38 dan 40

Perhatikan potongan kode program berikut.

int MERAH(int A, int B) {
    if (B == 0) {
        return A;
    } else {
        return MERAH(B, A % B);
    }
}

int PUTIH(int A, int B, int C) {
    if (C == 0) {
        return 0;
    } else if (MERAH(A, C) == B) {
        return 1 + PUTIH(A, B, C - 1);
    } else {
        return PUTIH(A, B, C - 1);
    }
}

int NUSANTARA(int A, int B) {
    return PUTIH(A, B, A);
}

38.

Dari 5 pilihan pemanggilan berikut, manakah yang hasil kembaliannya paling besar?

MERAH(24, 4)
MERAH(24, 9)
MERAH(24, 17)
MERAH(24, 18)
MERAH(24, 34)

39.

Berapakah hasil kembalian dari pemanggilan NUSANTARA(12, 3)?

Tuliskan jawaban dalam bentuk ANGKA.

40.

Berapakah hasil kembalian dari pemanggilan NUSANTARA(2025, 135)?

Tuliskan jawaban dalam bentuk ANGKA.

Olimpiade Sains Kota (OSK) 2025 - Komputer — Kujawab