Olimpiade Sains Kota (OSK) 2024 - Komputer
1.
Jawab →Pak Dengklek bermain sebuah puzzle klasik di mana ia harus menemukan 3 petak garis lurus berurutan yang memuat tulisan "OSN". Ketiga petak ini bisa berurutan secara horizontal, vertikal, maupun diagonal; serta boleh dibaca ke 8 arah: atas, bawah, kiri, kanan, kanan-atas, kanan-bawah, kiri-atas, maupun kiri-bawah.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | O | N | O | O | N | O | N | O | N | O | O | O | N | O | O | O | N | O | O | O |
| 2 | O | N | N | O | N | N | O | N | O | N | N | O | N | O | O | N | O | O | O | O |
| 3 | O | N | O | N | O | O | N | N | O | N | O | N | N | O | O | N | O | O | N | O |
| 4 | O | N | O | S | O | O | O | S | O | O | N | N | S | N | O | O | S | O | N | O |
| 5 | O | N | O | N | O | O | O | N | N | N | O | O | N | N | N | O | O | N | N | O |
| 6 | N | N | O | O | N | N | N | O | N | O | N | N | N | O | N | O | O | O | N | N |
| 7 | N | O | N | S | N | N | O | S | O | O | N | O | S | O | N | N | S | N | N | N |
| 8 | O | N | N | O | O | O | N | O | O | N | O | O | N | N | N | O | O | O | N | O |
| 9 | O | N | O | N | N | N | O | O | N | O | N | O | O | N | O | O | N | O | N | N |
| 10 | O | N | O | O | O | N | O | N | O | N | N | O | N | O | N | N | O | N | O | N |
Diketahui bahwa hanya terdapat satu lokasi tulisan "OSN" pada puzzle tersebut. Pak Dengklek meminta bantuan kepadamu: di kolom ke berapakah petak huruf 'O' yang memuat tulisan "OSN" tersebut?
Tuliskan jawaban dalam bentuk ANGKA.
2.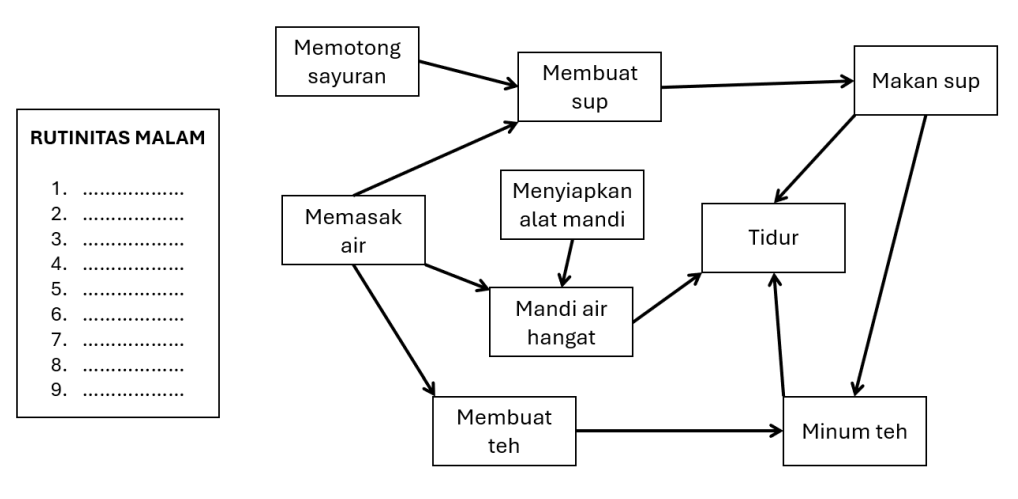
Jawab →Pak Dengklek ingin membuat sebuah rutinitas malam. Ada 9 kegiatan yang perlu ia rancang, namun ia menemukan bahwa terkadang sebuah kegiatan harus dilakukan sebelum sebuah kegiatan lainnya. Berikut merupakan ilustrasi dari persyaratan 9 kegiatan Pak Dengklek. Jika ada panah dari kegiatan A menuju kegiatan B, artinya kegiatan B hanya bisa dilakukan jika kegiatan A sudah pernah dilakukan sebelumnya.

Andaikan Pak Dengklek ingin kegiatan minum teh dilakukan seawal mungkin, maka pada urutan ke berapakah paling awal kegiatan "Minum teh" yang bisa ia rancang?
Tuliskan jawaban dalam bentuk ANGKA.
3.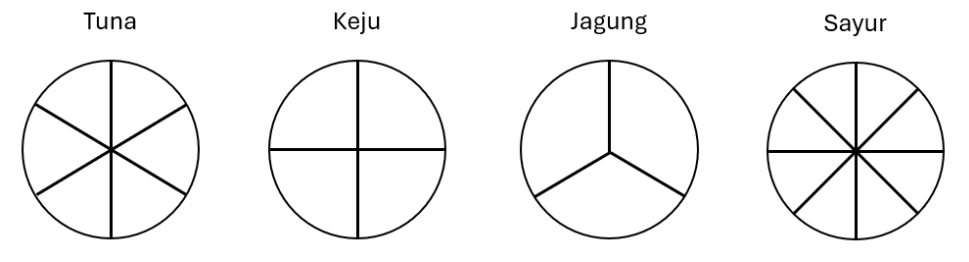
Jawab →Kwak dan Kwik suka sekali pizza. Pak Dengklek memesan 4 loyang pizza untuk mereka berdua: pizza tuna, pizza keju, pizza jagung, dan pizza sayur. Banyak potongan pizza masing-masing loyang pun berbeda-beda sebagai berikut.

Kwak sebenarnya tidak mau makan pizza keju, sedangkan Kwik sebenarnya tidak mau makan pizza tuna. Mereka tahu hal ini satu sama lain dan mereka ingin berebutan memakan sebanyak mungkin potongan pizza yang mereka sukai. Perhatikan bahwa mereka hanya fokus kepada banyaknya potongan dan tidak peduli dengan luas atau besarnya potongan tersebut.
Jika dimulai dari Kwak, Kwak dan Kwik berganti-gantian mengambil satu potong pizza mana pun yang mereka sukai (atau jika tidak ada lagi pizza yang ia sukai yang tersisa, maka ia akan berhenti makan — namun temannya tetap bisa makan jika memungkinkan), maka berapa potong pizza paling banyak yang Kwak bisa makan?
Tuliskan jawaban dalam bentuk ANGKA.
4.
Jawab →Terdapat 8 buah lampu yang berjejer dari kiri ke kanan dan dilabeli dengan huruf A, B, C, D, E, F, G, dan H. Pada awalnya, setiap lampu dalam kondisi mati.
Terdapat 10 bebek Pak Dengklek yang ingin bermain dengan lampu-lampu tersebut. Diketahui, bahwa masing-masing dari mereka memiliki lampu favorit masing-masing yang ditandai dengan centang pada tabel di bawah.
| Bebek | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| 2 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| 3 | ✓ | ✓ | ✓ | ✓ | ||||
| 4 | ✓ | ✓ | ✓ | ✓ | ||||
| 5 | ✓ | ✓ | ✓ | ✓ | ||||
| 6 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| 7 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 8 | ✓ | ✓ | ✓ | ✓ | ||||
| 9 | ✓ | ✓ | ✓ | |||||
| 10 | ✓ | ✓ | ✓ | ✓ |
Pak Dengklek memilih 9 dari 10 bebeknya. Untuk setiap bebek yang terpilih, satu per satu, ia akan mengganti seluruh status lampu-lampu favoritnya: jika sebelumnya mati, maka akan berubah menjadi menyala; jika sebelumnya menyala, maka akan berubah menjadi mati.
Jika ternyata kondisi akhirnya adalah hanya lampu A dan G yang menyala, bebek nomor berapakah yang tidak dipilih oleh Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
5.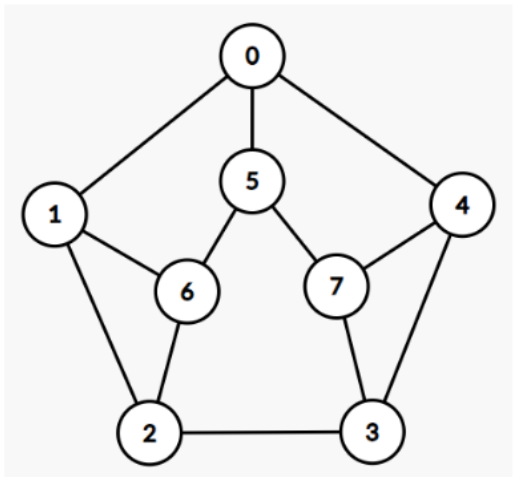
Jawab →Sebagai walikota, Pak Dengklek ingin mengadakan parade bebek di kotanya. Kota tersebut memiliki denah jalan sebagai berikut. Lingkaran menunjukkan persimpangan jalan dan garis menunjukkan jalan.

Sebuah parade akan dimulai dari suatu persimpangan jalan tertentu dan berakhir di suatu persimpangan jalan tertentu melalui serangkaian jalan-jalan yang terhubung. Agar seluruh lapisan masyarakat dapat menikmati parade bebek, Pak Dengklek ingin menjamin bahwa seluruh jalan pernah dilewati oleh parade bebek. Namun, karena masalah anggaran, setiap jalan hanya dapat dilewati maksimal satu kali. Perhatikan bahwa setiap persimpangan jalan tetap dapat dikunjungi lebih dari satu kali.
Untuk mengatasi masalah tersebut, Pak Dengklek memiliki ide untuk mengadakan parade bebek selama beberapa hari. Dalam satu hari, akan ada satu parade bebek yang diadakan oleh Pak Dengklek, dan Pak Dengklek dapat menentukan bagaimana parade bebek tersebut akan berjalan. Ingat bahwa apabila suatu jalan sudah dilewati oleh parade bebek pada suatu hari, maka jalan tersebut juga tidak boleh dilewati oleh parade bebek pada hari-hari lainnya.
Berapakah minimal hari yang diperlukan oleh Pak Dengklek agar seluruh jalan dijamin pernah dilewati oleh parade bebek?
Tuliskan jawaban dalam bentuk ANGKA.
6.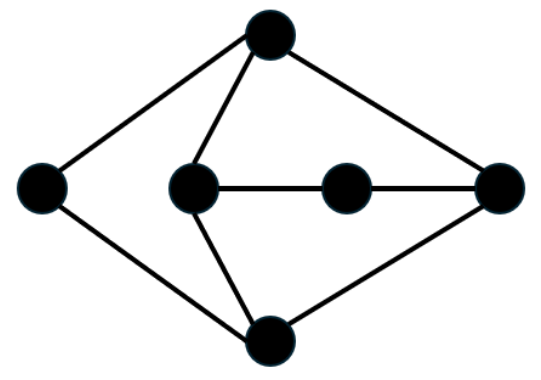
Jawab →Pak Dengklek mengajari bebek-bebeknya untuk menggambar denah desa masa kecilnya. Pak Dengklek mengatakan bahwa di desa tersebut hanya terdapat 6 buah rumah yang dihubungkan oleh 8 ruas jalan sebagai berikut:
Rumah 1 terhubung ruas jalan dengan rumah 2, 3, dan 4.
Rumah 2 terhubung ruas jalan dengan rumah 1, 3, dan 5.
Rumah 3 terhubung ruas jalan dengan rumah 1, 2, dan 6.
Rumah 4 terhubung ruas jalan dengan rumah 1 dan 6.
Rumah 5 terhubung ruas jalan dengan rumah 2 dan 6.
Rumah 6 terhubung ruas jalan dengan rumah 3, 4, dan 5.
Bebek-bebek Pak Dengklek menggambar denahnya dengan lingkaran yang menunjukkan rumah dan garis yang menunjukkan ruas jalan. Namun karena mereka usil, mereka tidak menuliskan nomor rumah masing-masing.

BENAR atau SALAH: Jika nomor-nomor rumahnya dilabeli secara tepat, maka denah tersebut bisa jadi sudah sesuai dengan denah yang diinginkan oleh Pak Dengklek.
Tuliskan jawaban dalam bentuk BENAR/SALAH dengan huruf kapital.
7.
Pak Dengklek sedang memilih-milih kelereng. Tiap kelereng memiliki 4 sifat, namun hanya kelereng dengan kombinasi sifat tertentu saja yang akan dipilih. Tabel di bawah ini menunjukkan kelereng-kelereng Pak Dengklek.
Ukuran | Warna | Bahan | Desain | Terpilih/Tidak |
|---|---|---|---|---|
Kecil | Merah | Batu | Berkilau | Tidak Terpilih |
Kecil | Merah | Batu | Mosaik | Tidak Terpilih |
Kecil | Merah | Logam | Berkilau | Terpilih |
Kecil | Merah | Logam | Mosaik | Tidak Terpilih |
Kecil | Kuning | Batu | Berkilau | Terpilih |
Kecil | Kuning | Batu | Mosaik | Terpilih |
Kecil | Kuning | Logam | Berkilau | Terpilih |
Kecil | Kuning | Logam | Mosaik | Terpilih |
Besar | Merah | Batu | Berkilau | Tidak Terpilih |
Besar | Merah | Batu | Mosaik | Tidak Terpilih |
Besar | Merah | Logam | Berkilau | Tidak Terpilih |
Besar | Merah | Logam | Mosaik | Tidak Terpilih |
Besar | Merah | Logam | Berkilau | Tidak Terpilih |
Besar | Kuning | Batu | Berkilau | Tidak Terpilih |
Besar | Kuning | Batu | Mosaik | Terpilih |
Besar | Kuning | Logam | Berkilau | Tidak Terpilih |
Besar | Kuning | Logam | Mosaik | Tidak Terpilih |
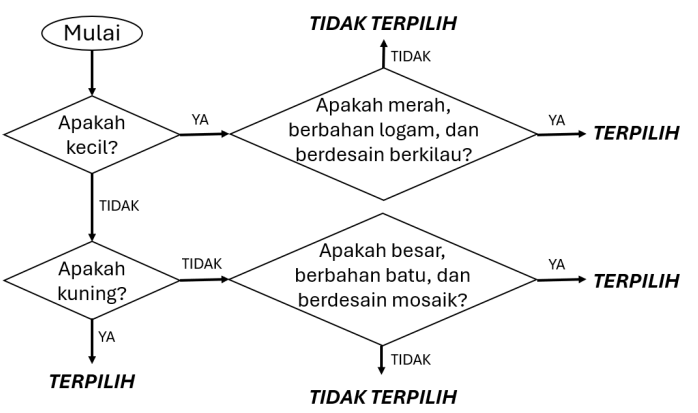
Agar lain kali Pak Dengklek tidak lupa saat hendak memilih kelereng-kelereng yang terpilih, Pak Dengklek membuat sebuah diagram. Dari 5 pilihan berikut, manakah yang dapat digunakan Pak Dengklek untuk memilih kelereng?
A
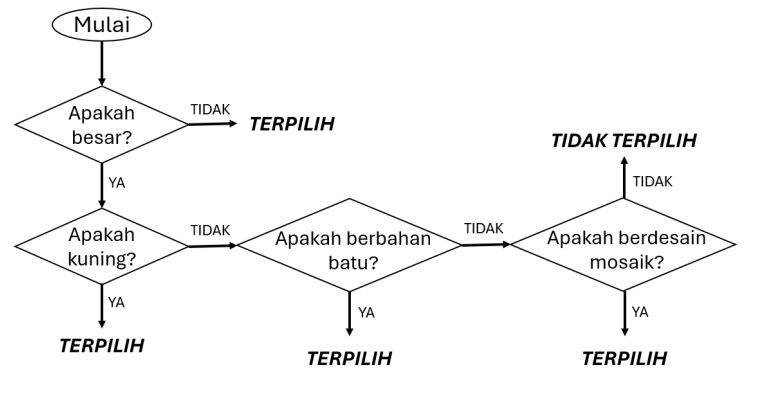
B
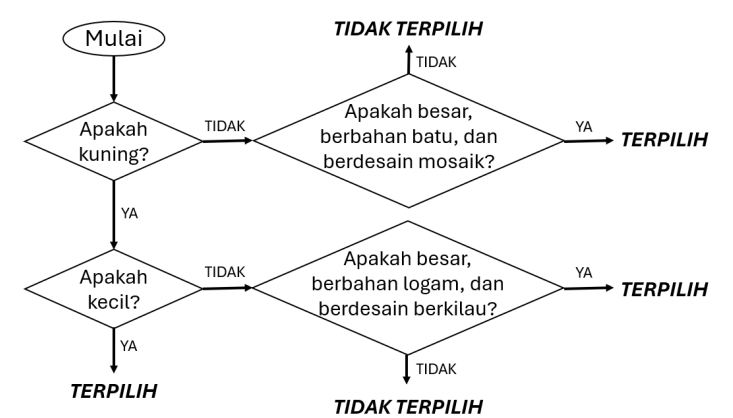
C
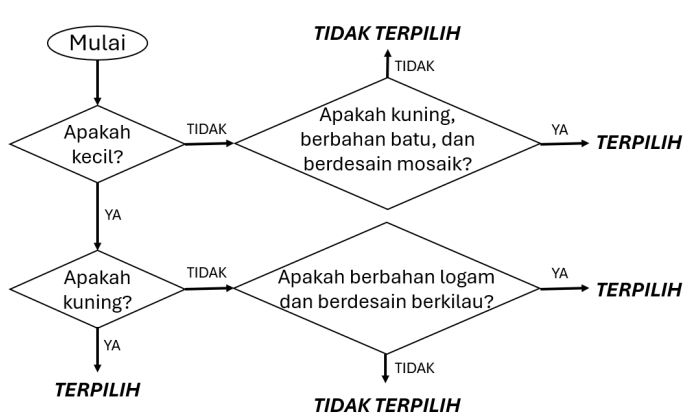
D
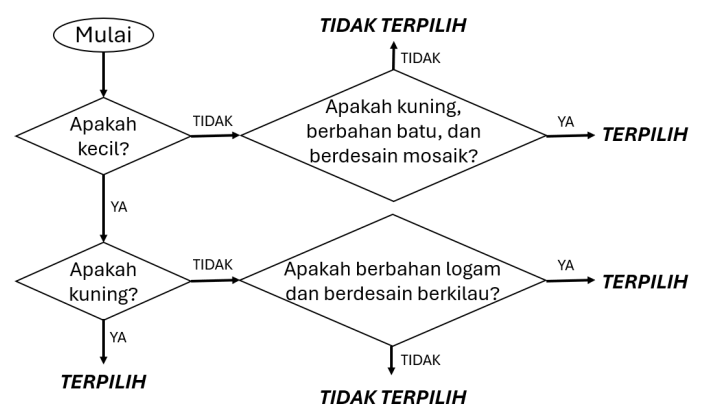
E
8.
Jawab →Pak Dengklek sedang melatih 11 calon pemain sepak bola. Pada latihan kali ini, Pak Dengklek ingin agar tiap calon pemain dapat menilai calon-calon pemain lain secara objektif. Pak Dengklek akan menunjuk beberapa calon-calon pemain tersebut menjadi komite audit.
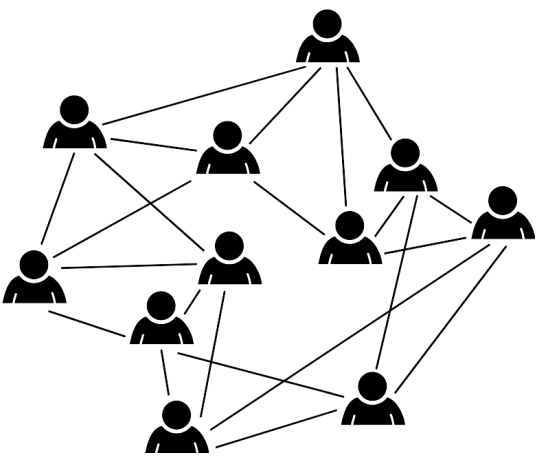
Diketahui bahwa antar calon pemain mungkin mempunyai hubungan pertemanan yang kuat dengan calon pemain lain (misalnya karena sudah berteman sejak lama). Dua calon pemain yang mempunyai hubungan kuat dihubungkan oleh sebuah garis seperti terlihat pada diagram berikut.

Jika anggota komite audit terdiri dari calon-calon pemain yang tidak mempunyai hubungan dengan anggota komite audit lainnya. Berapa paling banyak jumlah anggota komite audit yang mungkin?
Tuliskan jawaban dalam bentuk ANGKA.
9.
Jawab →Pak Dengklek dan Pak Ganesh bergiliran memainkan permainan "mengambil daun". Daun-daun ditumpuk pada dua piring: A dan B. Pada piring A terdapat 2 lembar daun dan pada piring B terdapat 3 lembar daun.

Saat gilirannya, pemain harus mengambil 1 atau lebih daun dari salah satu piring. Pemenang permainan ini adalah pemain yang mengambil daun terakhir dari 5 lembar daun yang ada.
Dari 5 skenario kondisi awal permainan berikut, manakah yang menjamin kemenangan Pak Dengklek?
Pak Dengklek memulai permainan dengan mengambil 1 daun dari piring A
Pak Dengklek memulai permainan dengan mengambil 2 daun dari piring A
Pak Dengklek memulai permainan dengan mengambil 2 daun dari piring B
Pak Ganesh memulai permainan dengan mengambil 1 daun dari piring A
Pak Ganesh memulai permainan dengan mengambil 1 daun dari piring B
10.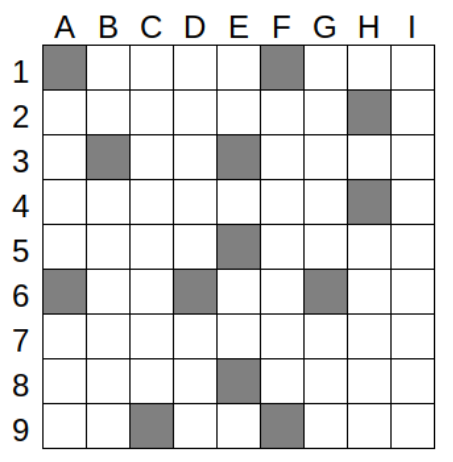
Jawab →Terdapat halaman berukuran 9x9 petak yang tiap petaknya dinyatakan dengan warna putih jika petak tersebut kosong, atau warna gelap jika petak tersebut basah; sebagai berikut.

Pak Dengklek akan meletakkan bebeknya di salah satu petak kosong dan memintanya untuk menghadap ke salah satu dari empat kemungkinan arah. Lalu, Pak Dengklek akan meminta bebeknya untuk melakukan 5 perintah berikut:
Bergerak maju sebanyak 2 petak
Berputar 90 derajat ke kiri (di petak yang sama)
Bergerak maju sebanyak 4 petak
Berputar 90 derajat ke kanan (di petak yang sama)
Bergerak maju sebanyak 2 petak
Jika Pak Dengklek ingin bebeknya tidak keluar dari halaman maupun tidak menginjak petak basah saat melakukan seluruh perintahnya, berapa banyak petak berbeda yang mungkin sebagai tempat awal peletakan bebek?
Tuliskan jawaban dalam bentuk ANGKA.
Deskripsi Untuk Soal Nomor 11 dan 13
Dalam sebuah pertandingan sepak bola, terdapat beberapa tim yang saling bertanding satu sama lain. Tim-tim tersebut diberi indeks berupa huruf alfabet (A hingga Z), dan setiap pasang tim akan saling bertanding tepat satu kali. Dalam setiap pertandingan, tim yang menang (tim yang mencetak gol lebih banyak) akan mendapatkan 3 poin. Jika ternyata pertandingan berakhir seri (kedua tim mencetak banyak gol yang sama), maka kedua tim mendapatkan 1 poin.
Anda akan diberikan hasil beberapa pertandingan. Tugas Anda adalah menentukan tim mana yang memimpin klasemen (tim dengan jumlah poin tertinggi). Jika terdapat lebih dari satu tim yang memiliki poin tertinggi di klasemen, pilih tim dengan indeks terkecil secara alfabetik.
11.
Jawab →Misalkan terdapat 4 tim yang sedang bertanding: C, E, R, dan I; dan diketahui hasil pertandingannya adalah sebagai berikut:
| Pertandingan Ke- | Tim Pertama | Tim Kedua | Gol yang Dicetak |
|---|---|---|---|
| 1 | C | E | 3 – 2 |
| 2 | E | R | 1 – 2 |
| 3 | I | E | 0 – 0 |
| 4 | I | C | 3 – 0 |
| 5 | R | C | 0 – 1 |
| 6 | R | I | 2 – 1 |
Tim manakah yang memimpin klasemen?
Tuliskan jawaban dalam bentuk HURUF KAPITAL.
12.
Jawab →Misalkan terdapat 5 tim yang sedang bertanding: C, E, R, I, dan A; dan diketahui hasil beberapa pertandingannya adalah sebagai berikut:
| Pertandingan Ke- | Tim Pertama | Tim Kedua | Gol yang Dicetak |
|---|---|---|---|
| 1 | C | E | 3 – 2 |
| 2 | E | R | 1 – 2 |
| 3 | I | E | 0 – 0 |
| 4 | I | C | 3 – 0 |
| 5 | R | C | 0 – 1 |
| 6 | R | I | 2 – 1 |
| 7 | A | C | ... |
| 8 | R | A | ... |
| 9 | I | A | ... |
| 10 | A | E | ... |
Perhatikan bahwa belum ada hasil pertandingan dari tim A melawan 4 tim lainnya. Jika tim A ingin berpeluang menjadi pemimpin klasemen setelah pertandingan ke-10, maka berapa paling sedikit dari 4 pertandingan tersebut yang harus dimenangkan oleh tim A?
Tuliskan jawaban dalam bentuk ANGKA.
13.
Jawab →Misalkan terdapat 26 tim yang sedang bertanding: A, B, C, dan seterusnya hingga Z. Diketahui bahwa di seluruh pertandingan:
- Jika indeks kedua tim sama-sama vokal atau sama-sama konsonan, maka tim dengan indeks terkecil secara alfabetik selalu menang.
- Jika indeks salah satu tim adalah vokal dan indeks tim lainnya adalah konsonan, maka pertandingan berakhir dengan seri.
Tim manakah yang memimpin klasemen?
Tuliskan jawaban dalam bentuk HURUF KAPITAL.
Deskripsi Untuk Soal Nomor 14 dan 16
Pak Blangkon memiliki 15 ekor ayam di pekarangan rumahnya: A, B, C, D, E, F, G, H, I, J, K, L, M, N, dan O. Diketahui bahwa ada beberapa pertemanan antara dua ekor ayam, yang didefinisikan sebagai P(X,Y) yang artinya ayam X dan ayam Y berteman. Jika ayam X dan ayam Y berteman, serta ayam Y dan ayam Z juga berteman, maka secara otomatis ayam X dan ayam Z juga berteman sehingga ayam X, ayam Y, dan ayam Z akan berada pada lingkaran pertemanan yang sama.
Pada suatu sore, Pak Blangkon ingin mengajak ayam-ayamnya bermain ke rumah Pak Dengklek. Namun karena keterbatasan tempat, Pak Blangkon tidak bisa mengajak semua ayamnya. Oleh karena itu Pak Blangkon akan mengajak beberapa ayamnya dengan ketentuan berikut:
- Minimal satu ekor ayam Pak Blangkon akan diajak.
- Ayam-ayam yang diajak berasal dari lingkaran pertemanan yang berbeda (agar tidak ada rasa iri antar ayam-ayamnya).
14.
Jawab →Diketahui bahwa informasi pertemanan antar ayam adalah sebagai berikut:
| P(A,B) | P(C,M) | P(E,G) | P(A,M) |
| P(D,J) | P(O,N) | P(B,O) | P(K,L) |
| P(D,I) | P(B,N) | P(L,D) | P(H,F) |
Ada berapa banyak lingkaran pertemanan ayam-ayam Pak Blangkon?
Tuliskan jawaban dalam bentuk ANGKA.
15.
Jawab →Jika untuk setiap lingkaran pertemanan harus ada perwakilan ayam yang diajak bermain, ada berapa banyak cara yang bisa dilakukan Pak Blangkon dalam memilih ayam-ayamnya?
Tuliskan jawaban dalam bentuk ANGKA.
16.
Jawab →Jika untuk setiap lingkaran pertemanan tidak harus ada perwakilan ayam yang diajak bermain, ada berapa banyak cara yang bisa dilakukan Pak Blangkon dalam memilih ayam-ayamnya?
Tuliskan jawaban dalam bentuk ANGKA.
Deskripsi Untuk Soal Nomor 17 dan 19
Pak Dengklek sedang belajar membuat biskuit. Ia membuat beberapa tipe biskuit berbeda yang masing-masing tipe diletakkan pada toples-toples yang berbeda. Karena bahan-bahan yang diperlukan untuk membuat masing-masing tipe biskuit berbeda, bisa jadi tiap toples berisi banyak butir biskuit yang berbeda pula.
Pak Dengklek kemudian mengundang bebek-bebeknya untuk mencicipi biskuit-biskuit buatannya. Satu per satu, para bebek bebas mengambil satu butir biskuit mana pun yang mereka ingin cicipi.
Agar Pak Dengklek mendapatkan ulasan yang cukup konkret, ia ingin semua tipe biskuit pernah dicicipi oleh sekian ekor bebek. Pak Dengklek ingin mencari tahu minimal bebek yang perlu diundang untuk mencicipi biskuit-biskuitnya.
17.
Jawab →Asumsikan Pak Dengklek sudah membuat 7 tipe biskuit berbeda, yang masing-masing terdiri dari 5 butir biskuit.
Jika Pak Dengklek ingin semua tipe biskuit pernah dicicipi oleh setidaknya 1 ekor bebek, berapa minimal bebek yang perlu diundang oleh Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
18.
Jawab →Asumsikan Pak Dengklek sudah membuat 100 tipe biskuit berbeda. Biskuit tipe 1 terdiri dari 10 butir, biskuit tipe 2 terdiri dari 20 butir, biskuit tipe 3 terdiri dari 30 butir, dan seterusnya hingga biskuit tipe 100 terdiri dari 1000 butir.
Jika Pak Dengklek ingin semua tipe biskuit pernah dicicipi oleh setidaknya 5 ekor bebek, berapa minimal bebek yang perlu diundang oleh Pak Dengklek?
Tuliskan jawaban dalam bentuk ANGKA.
19.
Jawab →Asumsikan Pak Dengklek sudah membuat 3 tipe biskuit berbeda. Biskuit tipe 1 terdiri dari A butir, biskuit tipe 2 terdiri dari B butir, dan biskuit tipe 3 terdiri dari C butir. Diketahui bahwa total biskuit yang dibuat Pak Dengklek adalah 25 (dengan kata lain, A + B + C = 25).
Jika diketahui pula bahwa Pak Dengklek perlu mengundang minimal 20 ekor bebek agar semua tipe biskuit pernah dicicipi oleh setidaknya 1 ekor bebek, maka berapa banyak triplet <A,B,C> berbeda yang mungkin?
Tuliskan jawaban dalam bentuk ANGKA.
Deskripsi Untuk Soal Nomor 20 dan 22
Terdapat dua buah meja berbentuk poligon beraturan: satu meja berwarna hitam, serta satu meja berwarna putih dengan suatu tanda panah di atasnya. Setiap sisi meja, baik meja hitam maupun meja putih, memiliki panjang yang sama, panjang sisi meja hitam dan sisi meja putih pun sama.
Pada awalnya, meja hitam terletak di tengah-tengah ruangan dan tidak dapat digerakkan, sedangkan meja putih terletak tepat di sebelah Utara (UT) meja hitam sedemikian sehingga kedua sisi meja saling berhimpitan dan tanda panah di atas meja putih juga menunjukkan ke arah UT.
Anda kemudian memiliki ide usil yakni menggelindingkan meja putih searah jarum jam mengelilingi meja hitam, dan menjamin bahwa kedua meja selalu bersentuhan, selama beberapa putaran.
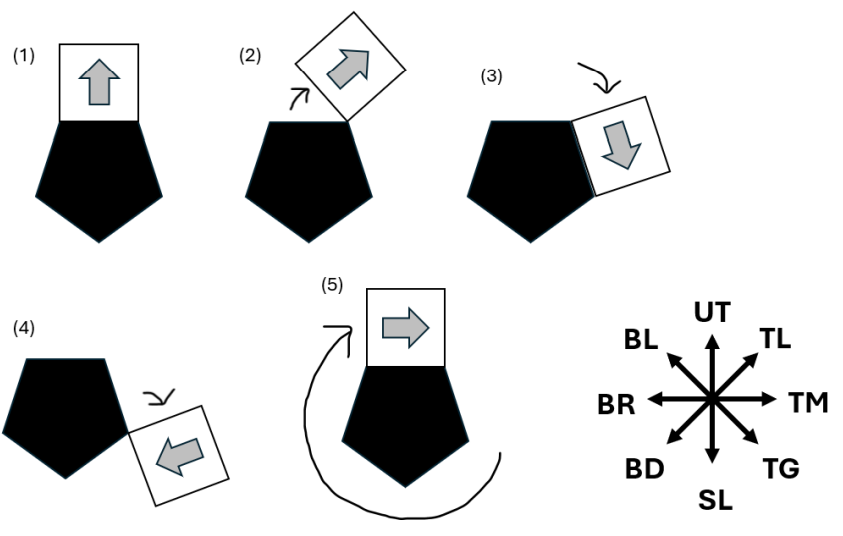
Sebagai contoh, berikut ini ilustrasi jika Anda menggelindingkan meja putih yang berbentuk segi-4 mengelilingi meja hitam yang berbentuk segi-5 sebanyak 1 putaran. Perhatikan bahwa setelah 1 putaran tersebut, tanda panah pada meja putih sekarang menunjukkan ke arah Timur (TM).
20.
Jawab →Jika Anda menggelindingkan meja putih yang berbentuk segi-8 mengelilingi meja hitam yang berbentuk segi-11 sebanyak 1 putaran, ke mana arah yang ditunjuk oleh tanda panah pada meja putih pada akhirnya?
Tuliskan jawaban dalam bentuk DUA HURUF KAPITAL yang menyatakan singkatan mata angin seperti pada ilustrasi.
21.
Jawab →Jika Anda menggelindingkan meja putih yang berbentuk segi-8 mengelilingi meja hitam yang berbentuk segi-13 sebanyak 17 putaran, ke mana arah yang ditunjuk oleh tanda panah pada meja putih pada akhirnya?
Tuliskan jawaban dalam bentuk DUA HURUF KAPITAL yang menyatakan singkatan mata angin seperti pada ilustrasi.
22.
Jawab →Jika Anda menggelindingkan meja putih yang berbentuk segi-123 mengelilingi meja hitam yang berbentuk segi-456 sebanyak X putaran, berapakah bilangan positif terkecil X sehingga arah yang ditunjuk oleh tanda panah pada meja putih pada akhirnya menghadap tepat ke Utara (UT) kembali?
Tuliskan jawaban dalam bentuk ANGKA.
Deskripsi Untuk Soal Nomor 23 dan 25
Terdapat 31 kursi di dalam sebuah kelas. Kursi-kursi tersebut ditempatkan dengan bentuk lingkaran dan diberi angka dari 1 hingga 31 seperti gambar berikut.
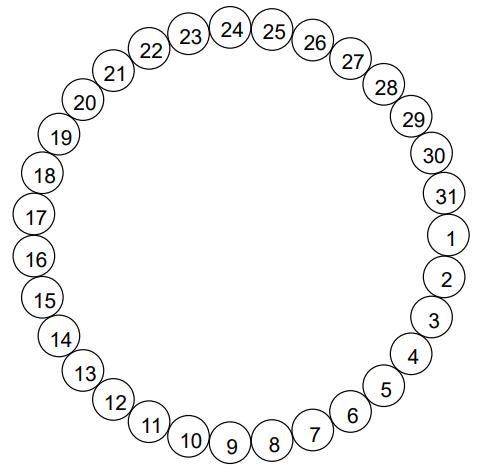
Para siswa awalnya berada di luar kelas lalu bermain permainan berikut:
Siswa masuk ke dalam kelas satu per satu.
Siswa duduk di kursi yang angkanya sesuai dengan tanggal lahirnya.
Jika kursi yang dituju telah terisi, ia akan berjalan sepanjang lingkaran searah jarum jam, hingga ia menemukan sebuah kursi kosong yang akhirnya ia duduki.
Sebagai contoh, Gita dan Sita adalah kembar yang lahir pada 20 April, Arun lahir pada 21 Januari, dan Zubin lahir pada 22 September.
Jika mereka datang dengan urutan: Gita, Sita, Zubin, dan Arun; maka Gita duduk pada kursi 20, Sita pada kursi 21, Zubin pada kursi 22, dan Arun pada kursi 23.
Jika mereka datang dengan urutan: Sita, Arun, Zubin, dan Gita; maka Sita duduk pada kursi 20, Arun pada kursi 21, Zubin pada kursi 22, dan Gita pada kursi 23.
23.
Jawab →Diketahui bahwa terdapat 6 siswa yang akan bermain permainan tersebut:
| Nama | Ulang Tahun |
|---|---|
| Andi | 11 Mei |
| Benny | 12 Februari |
| Chacha | 14 September |
| David | 11 Agustus |
| Ela | 13 April |
| Fatima | 12 Juli |
Jika mereka masuk ke dalam kelas dengan urutan: Andi, Benny, Chacha, David, Ela, dan Fatima; maka di kursi ke berapakah Ela duduk?
Tuliskan jawaban dalam bentuk ANGKA.
24.
Jawab →Diketahui bahwa terdapat 6 siswa yang sudah selesai bermain permainan tersebut:
| Nama | Ulang Tahun | Duduk di |
|---|---|---|
| Andi | 11 Mei | Kursi 13 |
| Benny | 12 Februari | Kursi 12 |
| Chacha | 14 September | Kursi 14 |
| David | 11 Agustus | Kursi 11 |
| Ela | 13 April | Kursi 15 |
| Fatima | 12 Juli | Kursi 16 |
Dari 5 pernyataan berikut, manakah yang tidak akan pernah mungkin benar?
- Chacha adalah orang yang pertama kali masuk ke dalam kelas
- Fatima adalah orang yang terakhir kali masuk ke dalam kelas
- Andi masuk ke dalam kelas sebelum Fatima
- Ela masuk ke dalam kelas sebelum Benny
- Benny masuk ke dalam kelas sebelum David
25.
Jawab →Diketahui bahwa terdapat 6 siswa yang sudah selesai bermain permainan tersebut:
| Nama | Ulang Tahun | Duduk di |
|---|---|---|
| Andi | 11 Mei | Kursi 13 |
| Benny | 12 Februari | Kursi 12 |
| Chacha | 14 September | Kursi 14 |
| David | 11 Agustus | Kursi 11 |
| Ela | 13 April | Kursi 15 |
| Fatima | 12 Juli | Kursi 16 |
Berapa banyakkah urutan masuk siswa ke dalam kelas yang mungkin?
Tuliskan jawaban dalam bentuk ANGKA.