Olimpiade Sains Provinsi (OSP) 2014 - Komputer
1.
Lihat 6 jawaban →TOKI Camp 2014 kali ini diadakan di sebuah bukit. Seorang alumni TOKI mendaki bukit tersebut dengan berjalan dengan kecepatan 1,5 km/jam. Ketika menuruni bukit tersebut, ia berjalan tiga kali lebih cepat. Jika waktu yang dibutuhkan untuk melakukan perjalanan bolak-balik dari kaki bukit ke puncak bukit dan kembali ke kaki bukit adalah 6 jam, maka jarak antara kaki bukit dan puncak bukit adalah?
2.
Lihat 6 jawaban →Pada sebuah toples, terdapat 1 juta ekor bakteri. Pada setiap detiknya, setiap bakteri membelah diri menjadi tepat dua ekor bakteri, kemudian toples tersebut dimasukkan 1 juta ekor bakteri tambahan. (Pada detik pertama, ada 3 juta bakteri. Pada detik kedua, ada 7 juta bakteri.) Berapakah banyak bakteri pada detik ke 14?
Deskripsi Untuk Soal Nomor 3 dan 5
Dari 100 orang peserta OSN komputer, diketahui 40 orang menyukai soal kombinatorika, 40 orang suka soal teori bilangan, dan 48 orang suka teka-teki silang. Diketahui pula 4 orang suka ketiganya.
3.
Lihat 3 jawaban →Jika peserta yang hanya suka dengan satu jenis soal saja ada 50 orang, berapa orang yang hanya suka dengan dua jenis soal?
4.
Jawab →Berdasarkan jawaban soal sebelumnya, jika yang hanya menyukai soal kombinatorika adalah 14 orang, berapa orang yang suka kombinatorika dan teori bilangan, atau suka kombinatorika dan teka-teki silang, namun tidak ketiganya?
5.
Jawab →Bila peserta yang menyukai persis hanya 2 jenis soal adalah 31 orang, berapa orang yang tidak suka satupun dari ketiga jenis soal tersebut?
6.
Lihat 5 jawaban →Diberikan sebuah fungsi F(x) = 1 - 2x - 3x2 - 4x3 dengan x bilangan bulat dimulai dari 1 sampai dengan 30. Berapakah x yang memenuhi F(x) = -20552?
Petunjuk: semakin besar nilai x, maka semakin kecil nilai F(x).
7.
Lihat 2 jawaban →Dewangga memiliki 2 ekor semut dan 2 ekor anak semut. Suatu hari, para semut dan anaknya ingin menyeberangi sungai dengan menggunakan perahu daun. Namun, perahu daun tersebut hanya cukup menampung 2 ekor anak semut atau seekor semut dewasa. Hebatnya, para semut Dewangga sudah terlatih untuk mendayung perahu daun, sehingga tiap kali menyeberang minimal harus ada 1 ekor semut atau 1 ekor anak semut yang mendayung. Untuk menyeberangkan keempat ekor semut, berapa kali minimum perahu tersebut harus menyeberangi sungai (bolak-balik dihitung 2 kali penyeberangan)?
Deskripsi Untuk Soal Nomor 8 dan 9
Budi ingin bermain Loncat Berhadiah. Permainan dimainkan pada sebuah kotak berukuran R x C petak. Petak kiri atas dinomori (1, 1) dan petak kanan bawah dinomori (R, C). Pada setiap petak terdapat sebuah bilangan. Budi memulai permainan dengan memilih salah satu petak pada kolom 1. Dari suatu petak (r, c), Budi harus berpindah ke petak (r, c+1), (r+1, c+1), atau (r-1, c+1). Apabila Budi sudah berada pada kolom C, permainan berakhir. Budi mendapat poin berupa jumlah seluruh bilangan yang terdapat pada petak-petak yang dilalui Budi.
8.
Lihat 5 jawaban →Berapa poin maksimum yang dapat diperoleh Budi pada kotak permainan di bawah ini?
| 2 | 5 | 5 | 1 |
| 3 | 1 | 4 | 2 |
| 4 | 2 | 3 | 3 |
9.
Jawab →Berapa poin maksimum yang dapat diperoleh Budi pada kotak permainan di bawah ini?
| 1 | 7 | 9 | 10 | 3 | 5 |
| 4 | 2 | 4 | 8 | 4 | 3 |
| 5 | 3 | 5 | 5 | 6 | 1 |
| 2 | 4 | 6 | 9 | 3 | 2 |
| 3 | 5 | 6 | 1 | 2 | 5 |
10.
Lihat 3 jawaban →Heru selalu berkata jujur pada hari Senin, Selasa, dan Rabu. Heru selalu berkata bohong pada hari Kamis, Jumat, dan Sabtu. Pada hari Minggu, ia bisa berkata jujur atau bohong. Pada suatu hari, teman Heru, Kudo ingin menanyakan suatu informasi yang penting pada Heru. Sayangnya, Kudo lupa melihat kalender sehingga lupa tanggal dan hari pada saat itu. Tentu saja Kudo yang cerdas tidak langsung menanyakan pertanyaannya pada Heru. Setelah Kudo menanyakan beberapa pertanyaan, Heru menjawab, "Hari ini saya sedang berkata jujur, begitu pula esok hari. Hari ini bukan hari Kamis maupun Senin. Kemarin saya berkata bohong. Kemarin adalah hari Minggu". Pada hari apakah Kudo bertemu Heru?
11.
Lihat 4 jawaban →N orang berdiri membentuk lingkaran, dan menunggu pembagian hadiah. Penghitungan dimulai pada suatu titik dan disebut posisi pertama, posisi selanjutnya mengikuti arah jarum jam. Pada setiap penghitungan, K-1 orang akan dilewati dan orang ke K akan keluar dari lingkaran. Proses ini dilakukan berulang-ulang hingga tinggal 1 orang dalam lingkaran dan orang tersebut yang akan mendapatkan hadiah. Jika diberikan N = 20 dan K = 14, orang pada posisi berapa yang akan mendapatkan hadiah?
Contoh : N = 5 dan K = 2, maka urutan orang yang keluar mulai dari yang paling awal adalah 2, 4, 1, 5, sehingga yang akan mendapatkan hadiah adalah orang pada posisi 3.
12.
Lihat 1 jawaban →
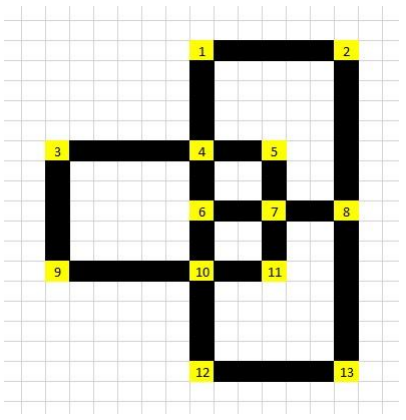
Di sebuah kota yang terdiri dari 13 persimpangan (yang diberi angka), terdapat jalan-jalan yang menghubungkan beberapa persimpangan. Fathin ingin berjalan-jalan dari tempat tinggalnya di persimpangan berlabel X ke suatu persimpangan berlabel Y. Y bisa saja sama dengan X. Tanpa dia sadari, rute yang dia tempuh dalam perjalanannya melewati semua jalan (bukan persimpangan) tepat satu kali. Berapakah label X terkecil yang mungkin ?
Deskripsi Untuk Soal Nomor 13 dan 14
Suatu hari Pak Dengklek sedang membangun rumah baru, ia ingin membuat dekorasi berupa sebuah persegi panjang dengan lebar 1 satuan. Ia memiliki dua jenis segitiga, yang pertama segitiga siku-siku sama kaki dengan panjang kaki 1 satuan, dan segitiga yang kedua berupa segitiga sama kaki gabungan dua segitiga yang pertama.
13.
Lihat 1 jawaban →Jika pak Dengklek membuat dekorasi dengan panjang 3 satuan, ada berapa cara untuk membuat dekorasi tersebut?
14.
Jawab →Selanjutnya pak Dengklek ingin membuat dengan panjang 8 satuan, ada berapa cara untuk membuat dekorasi tersebut?
15.
Lihat 2 jawaban →Terdapat 6 siswa dan 8 siswi di dalam sebuah kelas. Apabila suatu tim yang beranggotakan 5 orang akan dibentuk dari kelas tersebut. Berapa banyak kemungkinan komposisi isi tim apabila minimum terdapat 1 siswa dan 1 siswi di dalam tim tersebut?
Deskripsi Untuk Soal Nomor 16 dan 18
Walikota Budi ingin membuat sebuah rute transonjek di sebuah provinsi Bagus. Sebuah rute transojek harus memenuhi beberapa kriteria di bawah ini :
-
Sebuah rute harus menghubungkan semua kota-kota yang berada pada provinsi Bagus
-
Dari setiap kota hanya boleh terdapat tepat 1 jalur menuju setiap kota lainnya
-
Jumlah jalur yang dipakai harus berjumlah N-1 (N adalah jumlah kota)
-
Tidak diperbolehkan membuat jalur baru (hanya diperbolehkan menggunakan jalur yang telah disediakan)
- Apabila sebuah kota x terhubung dengan kota y, maka kota y juga terhubung dengan kota x
16.
Lihat 3 jawaban →Apabila dalam provinsi Bagus terdapat 7 kota A,B,C,D,E,F,G berapa banyak konfigurasi rute yang memenuhi jika jalur yang ada sebagai berikut?
-
Kota A terhubung dengan kota B dan C
-
Kota D terhubung dengan kota B, C , dan E
-
Kota E terhubung dengan kota F dan G
- Kota F terhubung dengan G
17.
Jawab →Apabila dalam provinsi Bagus terdapat 12 kota A,B,C,D,E,F,G,H,I,J,K, dan L berapa banyak konfigurasi rute yang memenuhi jika jalur yang ada sebagai berikut?
-
Kota B terhubung dengan kota A dan C
-
Kota D terhubung dengan kota C dan I
-
Kota E terhubung dengan kota C,F,G, dan H
-
Kota F terhubung dengan kota G
-
Kota I terhubung dengan kota H,J,dan L
- Kota K terhubung dengan kota J dan L
18.
Jawab →Apabila pada provinsi Bagus semua kota yang ada saling terhubung dengan kota lainnya berapa banyak konfigurasi rute transojek yang dapat dibentuk apabila jumlah kota yang ada dalam provinsi Bagus berjumlah 4?
19.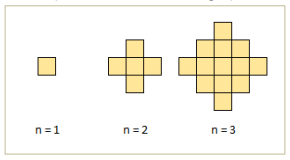
Lihat 3 jawaban →Perhatikan pola bangun berikut ini. Jika untuk n=3 terdapat 5 macam ukuran persegi panjang yang dapat dibentuk, {2×1, 3×1, 4×1, 5×1, 2×3}. Bujur sangkar tidak termasuk sebagai persegi panjang yang dimaksud di sini. Tentukan berapa banyak macam ukuran persegi panjang yang dapat dibentuk untuk n=100?

Catatan: a×b dan b×a, a≠b, dianggap sebagai ukuran persegi panjang yang sama.
20.
Lihat 1 jawaban →Pada suatu permainan kartu, terdapat 2 jenis kartu: kartu emas dan kartu perak. Permainan dilakukan oleh 1 orang pemain dengan tujuan mendapatkan kartu emas sebanyak-banyaknya. Berikut adalah aturan permainan tersebut:
-
Pada setiap putaran, pemain hanya dapat mengambil selembar kartu
-
Pemain tidak dapat mengambil 5 kartu perak secara berturut-turut
- Jika pada p+1 putaran sebelumnya pemain telah mengambil p+1 kartu perak secara berturut-turut, maka paling banyak p kartu emas baru boleh diambil secara berturutturut
Berapa jumlah maksimal kartu emas yang dapat diambil jika pemain bermain selama 613 putaran ?
21.
Lihat 3 jawaban →Ammar, Soko, Salvian, Ivan dan Rakina bermain ayam-bebek. Setiap anak menjadi ayam atau bebek, tetapi tidak kedua-duanya. Ayam selalu jujur, sementara bebek selalu berdusta. Ammar berkata bahwa Soko adalah ayam. Salvian berkata bahwa Ivan adalah bebek. Rakina berkata Ammar bukan bebek. Soko berkata Salvian bukan ayam. Ivan berkata bahwa Rakina dan Ammar adalah binatang yang berbeda. Berapakah banyaknya bebek dalam permainan ini?
Deskripsi Untuk Soal Nomor 22 dan 23
Pada suatu sore hari Budi sedang amat teramat bosan sehingga ia menciptakan sebuah permainan yang sangat inovatif yaitu "Lempar bola". Tujuan permainan ini sangat sederhana yaitu Budi hanya ingin memasukkan satu-satunya bola yang ia pegang sekarang ke dalam keranjang-keranjang yang terdapat dalam suatu tempat. Ketika dia berhasil memasukkan bola ke dalam suatu keranjang, maka Budi akan berjalan ke koordinat keranjang yang dia masukkan dan mengambil bola tersebut dan melemparkan bola tersebut ke keranjang lain yang belum dimasukkan dari posisi Budi sekarang. Budi ingin berjalan seminimum mungkin. Bantulah Budi untuk menghitung jarak minimum untuk memasukan bola ke semua keranjang.
22.
Lihat 8 jawaban →Berapa jarak minimum yang dapat ditempuh untuk memasukan bola ke semua keranjang apabila koordinat Budi sekarang dan koordinat keranjang seperti gambar dibawah ini?

23.
Jawab →Berapa jarak minimum yang dapat ditempuh untuk memasukan bola ke semua keranjang apabila koordinat Budi sekarang terdapat di titik 0 dan koordinat Keranjang terdapat di titik -20, -15, -9, -5, -3, 2, 3, 10, 13, 20?
24.
Lihat 3 jawaban →String adalah kumpulan dari karakter, sedangkan substring adalah string yang berturutan yang merupakan bagian dari string lain. Misal, "ABCDEF", "BCDE", dan "ABEC" adalah string. "CBBC" merupakan substring dari "ACBBCA" namun "CBCA" bukan merupakan substring dari "ACBBCA". Berapa banyak string yang terdiri dari huruf A, B dan C, yang memiliki panjang 8 dan tidak mengandung substring AB?
25.
Lihat 3 jawaban →Di sebuah peternakan terdapat beberapa jenis hewan. Ada yang pemakan tumbuh-tumbuhan, daging dan pemakan segala. Ada yang berkaki 2, berkaki 4 dan tidak berkaki. Jika suatu saat dipilih secara acak seekor hewan, kemungkinan terpilih hewan berkaki empat atau pemakan tumbuhan adalah 51/62, kemungkinan terpilih berkaki dua atau pemakan tumbuhan adalah 11/62, dan tidak mungkin terpilih hewan tanpa kaki yang pemakan segala ataupun pemakan tumbuhan yang berkaki. Jika di antara hewan tanpa kaki dipilih secara acak, kemungkinan didapatkan hewan yang pemakan tumbuhan adalah 1/2. Terakhir, peluang didapatkan hewan tanpa kaki atau pemakan tumbuhan adalah 1/31. Berapa peluang mendapatkan hewan berkaki empat?
26.
Lihat 6 jawaban →Perhatikan potongan program berikut!
var
i, j, total : integer;
begin
total := 0;
for i := 1 to 100 do
for j := 1 to 100 do
total := total + i - j;
writeln(total);
end.Berapakah nilai total di akhir program?
Deskripsi Untuk Soal Nomor 27 dan 28
Perhatikan potongan kode program berikut
function cimi(x,y:integer):integer;
begin
if (x + y = 0) then begin
cimi := 0;
end else if (x > y) then begin
cimi := y + cimi(x-1,y);
end else begin
cimi := x + cimi(x,y-1);
end;
end;27.
Lihat 4 jawaban →Berapakah nilai dari fungsi cimi(5,7)?
28.
Jawab →Berapakah nilai dari fungsi cimi(29,13)?
Deskripsi Untuk Soal Nomor 29 dan 30
Perhatikan potongan kode program berikut
function blossom(x : integer) : integer;
var
ans,i : integer;
begin
ans := 0;
for i := 1 to x do begin
ans := ans + i;
end;
blossom := ans;
end;
function bubble(x : integer) : integer;
var
ans,i : integer;
begin
ans := 0;
for i := 1 to x do begin
ans := ans + blossom(i);
end;
bubble := ans;
end;
function buttercup(x : integer) : integer;
var
ans,i : integer;
begin
ans := 0;
for i := 1 to x do begin
ans := ans + bubble(i);
end;
buttercup := ans;
end; 29.
Lihat 8 jawaban →Berapakah nilai dari buttercup(3)?
30.
Jawab →Berapakah nilai dari buttercup(6)?
Deskripsi Untuk Soal Nomor 31 dan 32
Perhatikan potongan kode program berikut
function kandang(ayam, kambing:integer):integer;
var rumput, sapi: integer;
begin
rumput:=(kambing-ayam) div 3;
sapi:=rumput*2;
if ayam > kambing then
kandang:= 0
else if (kambing-ayam < 3) then
kandang:= 2*(kambing-ayam)
else
kandang:= kandang(ayam,ayam+rumput)+
kandang(ayam+rumput,ayam+sapi)+
kandang(ayam+sapi,kambing);
end;31.
Lihat 6 jawaban →Berapakah nilai dari kandang(2,6)?
32.
Jawab →Berapakah nilai dari kandang(2014,3021)?
Deskripsi Untuk Soal Nomor 33 dan 34
Perhatikan potongan kode program berikut
var
i,j,x,baa:longint;
begin
x:=0;
baa:=10;
for i:=1 to baa do begin
for j:= 1 to i do begin
if i mod 2=1 then
x:=x-j
else
x:=x+j;
end;
end;
writeln(x);
end.33.
Lihat 7 jawaban →Apakah keluaran dari program di atas? .
34.
Jawab →Jika nilai baa pada awalnya diganti menjadi baa:=1000; maka keluaran program menjadi...
Deskripsi Untuk Soal Nomor 35 dan 36
Perhatikan potongan kode program berikut
var x,n,lala,lili,i:integer;
begin
x:=7; n:=x;
lala:=10;
lili:=12345;
for i:=0 to lili do
begin
x:=(x*n) mod lala;
end;
writeln(x);
end.35.
Lihat 2 jawaban →Apakah output dari program di atas ?
36.
Jawab →Apabila pada baris ke-4 diganti lala:=100; dan x bernilai awal 9, maka, output apa yang akan dihasilkan?
Deskripsi Untuk Soal Nomor 37 dan 38
Perhatikan potongan kode program berikut
var x:integer;
function lala(lili:integer):integer;
var abc,i:integer;
begin
abc:=0;
if (lili mod 5 = 0) then
begin
for i:=1 to 7 do abc:=abc+lala(lili div 5);
end else if (lili mod 3 = 0) then
begin
for i:=1 to 5 do abc:=abc+lala(lili div 3);
end else if (lili mod 2 = 0) then
begin
abc:=lala(lili div 2)+lala(lili div 2);
end;
if (lili=1) then lala:=1 else
lala:=abc;
end;
begin
x:=25;
writeln(lala(x));
end.37.
Lihat 2 jawaban →Apakah output dari program di atas ?
38.
Jawab →Apabila x bernilai 35, maka apakah output yang dihasilkan?
39.
Lihat 4 jawaban →Perhatikan potongan kode program berikut
var aku,sayang,kamu:integer;
begin
aku:=1;
sayang:=0;
kamu:=1;
while (sayang<=100) do
begin
aku:=aku+kamu;
inc(sayang);
inc(kamu); inc(kamu);
end;
writeln(aku);
end.Apakah output yang akan dihasilkan?
40.
Lihat 8 jawaban →Perhatikan potongan kode program berikut
var i,j:integer;
lala:boolean;
begin
for i:=2 to 100 do
begin
lala:=true;
j:=2;
while (j*j<=i) do
begin
if (i mod j = 0) then lala:=false;
inc(j);
end;
if (lala=true) then write(i);
end;
end.Apabila masing-masing digit dari seluruh output dijumlahkan, berapakah hasil penjumlahan digit-digit tersebut?
41.
Lihat 3 jawaban →Berapakah hasil yang dikembalikan fungsi tersebut pada pemanggilan iseng(500,100)?
Deskripsi Untuk Soal Nomor 42 dan 43
Perhatikan potongan kode program berikut
count := 0;
for i := 1 to n do
begin
x := i;
while (x > 0) do
begin
if (x mod 10 = 1) then
inc(count);
x := x div 10;
end;
end;
writeln(count);42.
Lihat 4 jawaban →Apakah output dari program apabila n = 12?
43.
Jawab →Apakah output dari program apabila n = 10000?
Deskripsi Untuk Soal Nomor 44 dan 45
Perhatikan potongan kode program berikut
function gembel(x,y : integer) : integer;
begin
if y=0 then gembel := x
else gembel := gembel(y,x mod y);
end;function wedhus(n : integer) : integer;
var pedhet : integer;
begin
pedhet := 0;
for i:= n-1 downto 1 do
begin
if gembel(n,i)=1 then pedhet := pedhet+1;
end;
wedhus := pedhet;
end;44.
Lihat 14 jawaban →Jika pada program utama terdapat statement untuk mencetak hasil dari wedhus(30), maka output yang ditampilkan adalah
45.
Jawab →Jika p adalah suatu bilangan prima, x adalah bilangan bulat positif, dan pangkat(p,x) adalah fungsi p pangkat x (px ), maka fungsi wedhus(pangkat(p,x)) akan menghasilkan output sesuai dengan rumus .... {tuliskan rumusnya sesederhana mungkin} (Gunakan variabel p, x, dan fungsi pangkat).
Deskripsi Untuk Soal Nomor 46 dan 47
Perhatikan potongan kode program berikut
var i,j: integer;
var board: array[0..5] of longint;
function kepo():integer;
var n:integer = 0;
begin
for i := 5 downto 0 do begin
n := n shl 1;
n := n + (board[i] mod 2);
end;
kepo:=n;
end;
procedure tambah();
begin
for i := 0 to 17 do
for j := 0 to 5 do
board[j] := board[j] + sqr(j+i);
end;
begin
for i := 0 to 5 do
board[i] := i;
tambah();
writeln(kepo());
end.46.
Lihat 5 jawaban →Berapakah output yang dihasilkan bila program tersebut dijalankan?
47.
Jawab →Berapakah nilai board[1] pada akhir program?
48.
Lihat 3 jawaban →Perhatikan potongan program di bawah ini!
var
data1 : array[1..10] of integer = (4,11,2,5,1,9,7,5,6,8);
data2,data3 : array[1..10] of integer;
i : integer;
begin
for i:= 1 to 10 do
data2[i] := 1;
for i:= 1 to 10 do
inc(data2[data1[i]]);
for i:= 2 to 10 do
data2[i] := data2[i] + data2[i-1];
for i:= 10 downto 1 do
begin
data3[data2[data1[i]]] := data1[i];
dec(data2[data1[i]]);
end;
for i:= 1 to 10 do
write(data3[i]);
end.Keluaran dari program di atas adalah
49.
Lihat 9 jawaban →Untuk menjawab soal pemrograman, perhatikan beberapa hal berikut:
-
Diberikan suatu persoalan, dan Anda diminta menuliskan program komputer dengan menggunakan pseudopascal atau bahasa pemrograman Pascal, C, atau C++.
-
Program komputer atau pseudopascal yang ditulis harus dapat menghasilkan output yang diminta dengan batasan yang sudah ditentukan.
-
Setiap persoalan terdiri atas deskripsi soal, batasan (waktu eksekusi, input, dan output), contoh input, dan contoh output.
- Dalam pemrograman komputer, diasumsikan bahwa satu detik waktu eksekusi setara dengan perulangan 103 kali instruksi.
JUMLAH DERET
Deskripsi:
Pada suatu hari, Pak Dengklek menemukan suatu pola penjumlahan dari N bilangan berikut:
1/3 + 2/21 + 3/91 + 4/273 + ...
Dengan menggunakan kalkulator, Pak Dengklek mulai menghitung. Untuk N=1, dihitung 1/3=0.33333. Untuk N=2, dihitung 1/3+2/21=0.42857. Nah, Pak Dengklek mulai pusing jika menghitung untuk N=1000000 (satu juta). Untuk itu, Pak Dengklek minta bantuan Anda membuatkan program menghitung deret tersebut.
Batasan:
-
Waktu eksekusi: 1 detik
-
Input: Input berupa sebuah bilangan bulat N dengan batasan 1<N<107.
- Output: Sebuah bilangan Riil hasil perhitungan jumlah deret dari N bilangan, yang ditulis dengan 5 digit desimal.
Contoh Input:
5
Contoh Output:
0.48387
50.
Lihat 6 jawaban →Untuk menjawab soal pemrograman, perhatikan beberapa hal berikut:
-
Diberikan suatu persoalan, dan Anda diminta menuliskan program komputer dengan menggunakan pseudopascal atau bahasa pemrograman Pascal, C, atau C++.
-
Program komputer atau pseudopascal yang ditulis harus dapat menghasilkan output yang diminta dengan batasan yang sudah ditentukan.
-
Setiap persoalan terdiri atas deskripsi soal, batasan (waktu eksekusi, input, dan output), contoh input, dan contoh output.
- Dalam pemrograman komputer, diasumsikan bahwa satu detik waktu eksekusi setara dengan perulangan 103 kali instruksi.
MEMOTONG PIPA
Deskripsi:
Pak Dengklek memiliki pipa sepanjang N meter, dan dia ingin memotongnya menjadi beberapa bagian sebanyak-banyaknya. Setiap potongan pipa harus memiliki panjang p meter, dimana 1<p<N, dan p adalah bilangan bulat. Hal ini menunjukkan bahwa panjang minimal potongan pipa adalah 1 meter. Disyaratkan bahwa tidak ada 3 potongan pipa manapun yang dapat membentuk segitiga. Pak Dengklek meminta bantuan Anda untuk membuat program menghitung maksimum banyaknya potongan pipa sesuai dengan syarat-syarat tersebut.
Batasan:
-
Waktu eksekusi: 1 detik
-
Input: Input berupa sebuah bilangan bulat N yang menunjukkan panjang pipa dalam satuan meter, dengan batasan 1<N<105.
- Output: Sebuah bilangan bulat banyaknya potongan pipa sesuai persyaratan dalam deskripsi soal.
Contoh Input:
7
Contoh Output:
4