Olimpiade Sains Provinsi (OSP) 2016 - Komputer
1.
Lihat 10 jawaban →Tentukan bilangan bulat positif terkecil x yang memenuhi fungsi f(x) = (4 + x)20 sehingga nilai digit terkanan dari nilai fungsi tersebut adalah 1.
2.
Lihat 5 jawaban →Gambar sebagai berikut adalah peta jalan antar kota di negeri 1001 Malam.
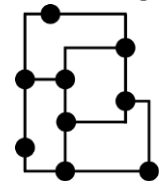
Karena banyak wisatawan yang mengagumi keindahan negeri 1001 Malam, sang raja berencana untuk membangun beberapa jalan tambahan supaya para wisatawan dapat bertamasya mengunjungi setiap kota dengan melewati setiap jalan hanya satu kali saja. Sebuah jalan tambahan yang dibangun hanya dapat menghubungkan tepat dua buah kota, dan dua buah kota dapat dihubungkan oleh lebih dari 1 (satu) jalan. Berapakah minimum banyak jalan tambahan yang perlu dibangun agar seorang wisatawan yang berawal dari sebuah kota dapat menggunakan setiap jalan antar kota tepat sekali (tidak harus kembali ke kota asal)?
3.
Lihat 6 jawaban →Pada suatu hari, terdapat seekor semut yang terperangkap di dalam sebuah kaleng yang terbuka. Semut tersebut mula-mula berada pada posisi awal yaitu titik A, dan ingin mencapai titik keluar (titik B) seperti pada gambar dengan merayap pada dinding kaleng.
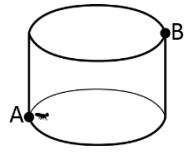
Jika diketahui jari-jari kaleng adalah 7 cm dan tinggi kaleng adalah 15 cm, berapakah jarak minimum yang perlu ditempuh oleh semut tersebut dari titik A untuk mencapai titik B? Tuliskan hasil jawaban dalam bentuk (pi) jika perlu.
4.
Lihat 3 jawaban →Pada sebuah arisan, jumlah orang yang hadir adalah 2016 orang, diberi identitas 1 sampai dengan 2016. Orang-orang tersebut akan dikelompokkan. Orang ke-i akan ditaruh sekompok dengan orang beridentitas i2 dan i3 kecuali jika i2 > 2016 atau i3 > 2016 Tentukan berapa banyak kelompok yang ada pada arisan tersebut.
5.
Lihat 1 jawaban →Pak Dengklek memiliki 6 buah pot bunga yang disusun berjajar dan siap ditanami 3 (tiga) jenis bunga yaitu melati, mawar, dan anggrek di pekarangan rumahnya. Ada berapa banyak cara pengisian 6 pot bunga tersebut sehingga pada 3 buah pot yang bersebelahan yang manapun, tidak ada 3 jenis bunga yang ketiganya berbeda?
6.
Lihat 2 jawaban →Pada sebuah permainan, seorang ksatria mula-mula berada pada posisi (1,1) dan hendak pergi ke posisi (6,6) untuk menyelamatkan seorang putri yang cantik. Setiap petak permainan dapat berisi vitamin atau racun.
- Petak yang berisi vitamin dilambangkan dengan bilangan positif pada peta, yaitu ramuan yang akan menambah kekuatan ksatria, atau
- Petak yang berisi racun dilambangkan dengan bilangan negatif pada peta, yaitu ramuan yang akan mengurangi kekuatan ksatria.
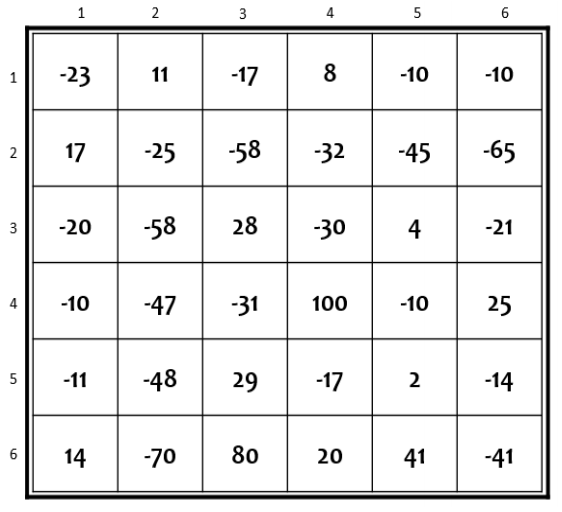
Pada permainan ini, ksatria hanya bisa berjalan ke arah timur atau selatan (tidak bisa melangkah secara diagonal). Ksatria tidak pernah boleh kehabisan kekuatan (kekuatan bernilai negatif atau 0) selama permainan berlangsung, termasuk pada awal permainan, dan semua ramuan pada petak-petak yang dilewati ksatria harus diminum. Tentukan jumlah kekuatan awal minimum yang harus dimiliki ksatria pada awal permainan agar ksatria tersebut dapat menyelamatkan sang putri dan memenangkan permainan!
7.
Lihat 1 jawaban →Berapakah banyak bilangan bulat positif berbeda yang habis membagi 337500?
8.
Lihat 2 jawaban →Pada sebuah pesta, terdapat 5 jenis pasangan makanan dan minuman yaitu jenis A, B, C, D, dan E. Setiap makanan jenis A, akan mempunyai pasangan minuman jenis A. Demikian juga untuk B, C, D, E. Pak Dengklek mendapat kesempatan untuk mencicipi semua jenis makanan dan minuman. Namun, terdapat aturan bahwa setiap minuman jenis X hanya dapat diminum jika dan hanya jika makanan jenis X sudah dimakan. Sebagai contoh, minuman jenis A hanya dapat diminum apabila makanan jenis A sudah dimakan. Berapa banyak kemungkinan urutan makan dan minum semua jenis makanan yang disediakan pada pesta tersebut? Anda dapat menuliskan jawaban dalam bentuk angka, atau dalam bentuk kombinasi, permutasi, dan faktorial.
9.
Lihat 2 jawaban →Diberikan sebuah larik (array) yang berisi 7 buah bilangan bulat yaitu: {42, 16, 40, 33, 0, 28, 41}. Pak Dengklek menginginkan sekumpulan bilangan (satu atau beberapa bilangan) yang jika dilakukan operasi XOR (exclusiveor terhadap representasi bit suatu bilangan) terhadap elemen-elemen larik tersebut satu demi satu, hasilnya adalah bernilai 0 (nol).
Pak Dengklek boleh menambahkan satu atau beberapa bilangan bulat ke dalam larik tersebut supaya keinginannya dapat tercapai. Namun ternyata, terdapat biaya yang perlu dibayar untuk menambahkan sekumpulan bilangan bulat, yaitu sebesar bilangan terbesar yang terdapat pada kumpulan bilangan tersebut. Sebagai contoh, bilangan bulat yang ingin ditambahkan = {25, 17, 1} maka biaya yang perlu dibayar adalah 25. Berapakah biaya terkecil yang perlu dibayar Pak Dengklek? (Jika ternyata Pak Dengklek tidak perlu menambahkan apa-apa, tuliskan 0).
10.
Lihat 6 jawaban →Ini adalah gambar Pak Dengklek dengan teman-temannya yang terdaftar di media sosial bernama TokiBook.
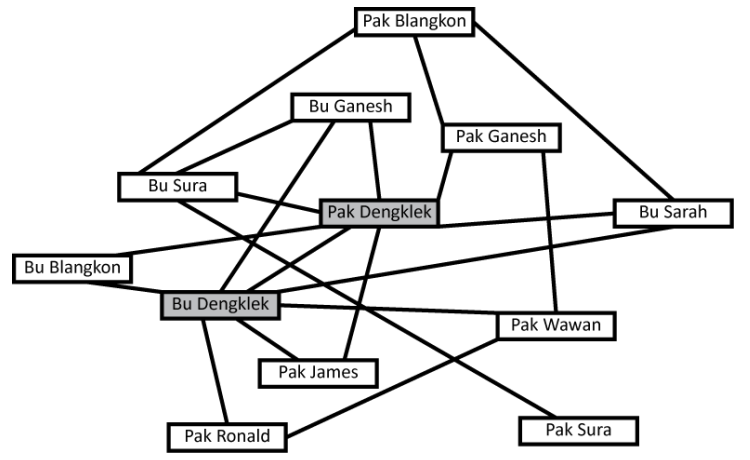
Pada TokiBook tersebut, sebuah garis menandakan adanya pertemanan antara dua orang. Pada media tersebut, seseorang dapat mengunggah sebuah foto, like sebuah foto, ataupun share foto yang diunggahnya. Peraturannya adalah sebagai berikut:
- Seseorang yang mengunggah foto, dapat memilih mau share ke teman yang mana, secara spesifik.
- Jika seseorang me-like foto anda, seluruh temannya dapat melihat foto anda.
Pak Dengklek ingin mengunggah sebuah foto, tetapi foto tersebut berbahaya apabila dilihat oleh Bu Dengklek. Kepada siapa saja Pak Dengklek dapat meng-share fotonya sehingga Bu Dengklek tidak melihat foto tersebut? Tuliskan nama-nama orang yang dapat melihat foto yang dikirim oleh Pak Dengklek dan tidak dapat dilihat oleh bu Dengkle, dipisahkan dengan koma.
11.
Lihat 3 jawaban →Ada suatu negara yang bernama negara TOKI. Mata uang negara TOKI tersebut unik, yaitu berbentuk koin yang masing-masing bernilai 2n (1, 2, 4, 8, 16, …. s.d. 2048). Pak Dengklek ingin membeli suatu barang dengan harga 714 dan harus membayar dengan uang pas. Berapa banyakkah pecahan mata uang minimum yang dibutuhkan untuk dapat membeli barang tersebut?
12.
Lihat 3 jawaban →Pak Dengklek adalah seseorang yang sangat suka dengan teka-teki. Pada suatu hari, ia membeli 10 bola, yang terdiri dari 3 warna putih, 4 warna merah, dan 3 warna hijau. Ia ingin mengambil beberapa bola tersebut secara bersamaan (boleh berapapun). Berapa banyaknya bola minimum yang diperlukan, agar dapat dijamin bahwa pak Dengklek mengambil minimal 2 bola untuk setiap warna?
13.
Lihat 5 jawaban →Pak Dengklek adalah orang yang suka teka-teki. Suatu hari ia berpikir untuk menghitung dari 1 sampai 2016 dengan menggunakan jari-jarinya.
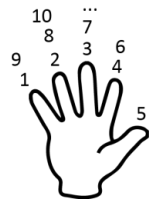
Pak Dengklek menghitung dengan menggunakan jari, dengan cara sebagai berikut: Proses menghitung diimulai dari 1, yaitu dengan jari kelingking; 2 dengan jari manis; 3 dengan jari tengah; 4 dengan jari telunjuk; 5 dengan jempol; 6 dengan jari telunjuk; 7 dengan jari tengah; 8 dengan jari manis; 9 dengan jari kelingking; 10 dengan jari manis; dan seterusnya. Jari apakah yang akan direpresentasikan saat Pak Dengklek menghitung angka 2016?
Deskripsi Untuk Soal Nomor 14 dan 15
Tusuk gigi di TOKI Fried Kitchen memang sering manjadi bahan mainan pelanggan. Suatu hari, karena bosan menunggu pesanannya, Pak Dengklek membuat persamaan matematika sederhana dengan 15 batang tusuk gigi yang ada di mejanya. Persamaan matematika yang dibuat pak Dengklek hanya dapat mengandung simbol-simbol pada gambar berikut, disertai juga jumlah batang tusuk gigi yang diperlukan untuk membuat masing-masing simbol. Suatu persamaan matematika merupakan sebuah string yang dibentuk dengan meng-konkatenasi (menyambungkan) simbol-simbol matematika yang dapat digunakan, misalnya 1+1=2 dan 1+4=2+3.

Persamaan matematika yang dibentuk Pak Dengklek harus memenuhi kriteria-kriteria berikut.
- Persamaan matematika tersebut dibuat dengan kurang dari atau sama dengan 15 batang tusuk gigi.
- Persamaan matematika tersebut mengandung tepat satu simbol ‘=’ (sama dengan).
- Ruas kiri dan ruas kanan mengandung paling sedikit satu simbol angka: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
- Nilai hasil penjumlahan atau angka pada ruas kiri sama dengan nilai hasil penjumlahan atau angka pada ruas kanan.
- Suatu simbol angka tidak dapat muncul tepat di sebelah simbol angka yang lain. Setiap angka satu digit
- Simbol ‘+’ (tambah) hanya dapat muncul di antara dua buah simbol angka.
14.
Lihat 2 jawaban →Berapa banyak string-persamaan-matematika berbeda yang dapat dibuat Pak Dengklek? Jika string yang merepresentasi persamaan berbeda, dihitung dua kali. Contoh dua buah persamaan “1 + 1 = 2” dan “2 = 1 +1” dihitung sebagai 2 (dua) persamaan.
15.
Jawab →Jika pernyataan “Persamaan matematika tersebut dibuat dengan kurang dari atau sama dengan 15 batang tusuk gigi.” diubah menjadi “Persamaan matematika tersebut dibuat dengan menggunakan tepat 15 batang tusuk gigi.”, berapa banyaknya string-persamaan-matematika berbeda yang dapat dibuat Pak Dengklek ?
16.
Lihat 4 jawaban →Pada sebuah papan catur berukuran 6x6, akan diletakkan 6 benteng putih dan 6 benteng hitam sedemikan sehingga benteng berwarna sama tidak boleh berada dalam baris yang sama dan pada kolom yang sama. Selain itu, Tidak boleh ada petak yang diisi lebih dari satu benteng. Berapa banyaknya cara meletakkan 6 benteng hitam dan 6 benteng putih dengan batasan tersebut ?
17.
Lihat 2 jawaban →Berapa banyaknya binary string dengan panjang 15 bit yang tidak mengandung substring "001"?
18.
Lihat 2 jawaban →Jika 1234 = 2x1 + 2x2 + 2x3 + 2x4 + 2x5 dimana x1, x2, . . . , x5 adalah bilangan cacah, dan x1 < x2 < . . . < x5. Tentukan nilai x1 + x2 +. . . + x5
19.
Lihat 2 jawaban →Pak Ganesh merahasiakan 2 bilangan bulat positif (x dan y, x <= y) dan lebih kecil dari 100. Dia memberitahukan hanya hasil penjumlahan kedua bilangan tersebut ke Pak Dengklek, dan hanya hasil perkalian kedua bilangan tersebut ke Bu Dengklek. Kemudian terjadi pembicaraan antara Pak Dengklek dan Bu Dengklek.
- Pak Dengklek : “Saya tidak tahu nilai kedua bilangan tersebut”.
- Bu Dengklek : “Saya juga tidak tahu”.
- Pak Dengklek : “Saya mengetahui bilangannya sekarang”.
- Bu Dengklek : “Saya juga”.
Perlu diketahui bahwa Pak Dengklek dan Bu Dengklek adalah orang sangat pintar, sehingga mengetahui nilai x dan nilai y tersebut. Berapakah nilai 5x + y?
Deskripsi Untuk Soal Nomor 20 dan 21
Pak Dengklek adalah seseorang yang sangat menyukai angka-angka. Pada suatu hari, ia berpikir sebagai berikut. Diberikan sebuah deretan angka (bisa tidak unik). Lalu, beberapa angka dari deretan tersebut dijumlahkan menghasilkan deret menaik dari 1,2,3, …. s.d. N.
Sebagai contoh, Jika kumpulan angka tersebut adalah (1,1,2), maka Pak Dengklek dapat membuat angka 1 dengan memilih (1), angka 2 dengan memilih (1,1) atau (2), angka 3 dengan memilih (1,2), angka 4 dengan memilih (1,1,2), tetapi tidak bisa memilih angka 5 karena tidak ada kemungkinan yang memenuhi. Dari penjumlahan tersebut, dapat dilihat bahwa angka 1 sampai dengan 4 dapat dibuat, karena itu nilai N yang memenuhi adalah 4.
20.
Lihat 3 jawaban →Diberikan sekuens (1,1,3,6,6,19,20), Berapakah nilai N yang memenuhi deskripsi di atas?
21.
Jawab →Diberikan sekuens (3,4,6,6). Berapa banyakkah bilangan minimum yang diperlukan agar N = 92 ?
Deskripsi Untuk Soal Nomor 22 dan 23
Dalam sebuah perusahaan, suatu proyek yang dipimpin oleh seorang pimpinan proyek akan dibagi-bagikan kepada 6 buah tim kecil yang beranggotakan sebagai berikut:
- Tim I : Abdul, Chika, Dono
- Tim II : Chika, Edgar, Gogo
- Tim III : Abdul, Farhan
- Tim IV : Abdul, Beni, Edgar
- Tim V : Beni, Chika, Farhan
- Tim VI : Beni, Dono, Gogo
Tiap awal bulan, setiap tim perlu melakukan rapat rutin bulanan yang wajib dihadiri seluruh anggota tim dengan lengkap. Tiap rapat rutin bulanan berdurasi selama 1 hari penuh. Karena alasan tersebut, untuk dua tim yang memiliki anggota yang sama perlu dijadwalkan rapat pada hari yang berbeda.
22.
Lihat 3 jawaban →Apabila pada 1 hari dapat dilakukan > 1 rapat rutin untuk tim-tim yang tidak memiliki anggota yang sama, berapa hari minimal supaya sang pimpinan proyek dapat memastikan bahwa seluruh tim sudah melakukan rapat bulanan?
23.
Jawab →Ternyata, terdapat sebuah modul proyek yang belum ditangani oleh tim I sampai VI sehingga sang pimpinan proyek membentuk sebuah tim kecil (tim VII) yang terdiri dari Abdul, Dono, dan Gogo. Berapa hari minimum supaya yang pimpinan proyek dapat memastikan bahwa tim I sampai VII sudah melakukan rapat bulanan?
24.
Lihat 4 jawaban →Sebagai pendekar, Pak Dengklek dan Pak Ganesh tidak boleh sakit. Supaya sehat, keduanya harus minum air putih 2 liter per hari. Pak Dengklek memiliki 2 buah gelas : satu berukuran 200 ml and satunya lagi berukuran 500 ml. Berapa banyak urutan minum Pak Dengklek dengan 2 buah gelas tersebut (tidak perlu dipakai semua) apabila ia ingin minum air putih tepat 2 liter? Urutan minum 200-200-200-200-200-500-500 dan 500-500-200- 200-200-200-200 dianggap berbeda.
25.
Lihat 3 jawaban →Sebagai pendekar, Pak Dengklek dan Pak Ganesh tidak boleh sakit. Supaya sehat, keduanya harus minum air putih 2 liter per hari. Pak Ganesh memiliki 3 buah gelas : satu berukuran 200 ml, satu berukuran 300 ml, and satunya lagi berukuran 500 ml. Berapa banyak urutan minum Pak Ganesh dengan 3 buah gelas tersebut (tidak perlu dipakai semua) apabila ia ingin minum air putih tepat 2 liter? Urutan minum 200-200-200-200-200-500- 500 dan 500-500-200-200-200-200-200 dianggap berbeda.
26.
Lihat 1 jawaban →Apa output program berikut apabila n = 6?
const MAXS = 10; var i, n : integer; A : array[1..10] of integer; procedure klik(); begin i := i-1; end; function klek(x : integer) : integer; begin if(x = MAXS) then klek := A[x] * A[1] else klek := A[x] * A[x+1]; end; function klok() : integer; var tmp : integer; begin if(i = 0) then klok := i else begin tmp := i; klik(); klok := klok() + klek(tmp); end; end; begin A[1] := 1; A[2] := 2; A[3] := 3; A[4] := 4; A[5] := 5; A[6] := 6; A[10] := 11; A[9] := 9; A[7] := 8; A[8]:=7; read(n); i := n; writeln(klok()); end.
27.
Lihat 4 jawaban →Diberikan potongan program sebagai berikut, berapakah hasil dari Proses(11)?
function Proses(x : integer) : integer; begin if(x <= 1) then Proses := x else Proses := Proses(x div 2 * x mod 2) + Proses(x div 2 + x mod 2); end;
28.
Lihat 1 jawaban →Diberikan fungsi sebagai berikut, berapakah nilai dari noan(8)?
function noan(n : integer) : integer; begin if(n < 4) then noan := n else noan := noan(n-1) + noan(n-2) + noan(n-4); end;
29.
Lihat 4 jawaban →Diberikan program sebagai berikut, berapa nilai array ar setelah pemanggilan mantaps(5)?
var ar : array[1..10] of integer = (1,6,2,3,4,7,2,4,2,1); procedure mantaps(n : integer); var i : integer; iNi : integer; temp : integer; begin if(n > 1) then begin iNi := n; for i := 1 to n-1 do begin if(ar[i] < ar[iNi]) then iNi := i; end; temp := ar[n]; ar[n] := ar[iNi]; ar[iNi] := temp; mantaps(n-1); end; end;
30.
Lihat 4 jawaban →Tuliskan keluaran program sebagai berikut :
var x,y: integer; begin x := 1; y := 0; while(x <= 10) do begin y := y + x; x := x + x; end; writeln(y); end.
31.
Lihat 1 jawaban →Tuliskanlah keluaran program sebagai berikut:
var ar : array[1..10] of integer = (4, 5, 10, 5, 51, 33, 49, 64, 2, 7); a, b, c, i : integer; begin a := -1; for i := 1 to 10 do begin if a = -1 then a := i else if ar[i] > ar[a] then a := i; end; b := -1; for i := 1 to 10 do begin if i <> a then begin if b = -1 then b := i else if ar[i] > ar[b] then b := i; end; end; c := -1; for i := 1 to 10 do begin if (i <> a) and (i <> b) then begin if c = -1 then c := i else if ar[i] > ar[c] then c := i; end; end; writeln(a, ' ', b, ' ', c); end.
32.
Lihat 2 jawaban →Tuliskanlah keluaran program berikut ini :
function meong(x: longint):integer; begin if (x = 0) then meong := 0 else if (x mod 2 = 1) and ((x div 2) mod 2 = 1) then meong := meong((x div 2) div 2) + 1 else meong := meong(x + 1) + 1; end; begin writeln(meong(888)); end.
33.
Lihat 1 jawaban →Perhatikan program Pascal berikut ini.
var arr: array [1..20] of integer = (303, 304, 365, 454, 487, 6, 12, 15, 78, 90, 155, 169, 183, 205, 209, 218, 5, 269, 282, 287); function get : integer; var m: integer; left, right: integer; begin if (arr[1] < arr[20]) then get := 1 else begin left := 1; right := 20; while (left < right) do begin m := (left+right) div 2; if (arr[1] <= arr[m]) then left := m+1 else right := m; end; get := left; end; end;
34.
Lihat 1 jawaban →Diberikan program sebagai berikut, ada berapa banyak elemen pada array tersebut yang bernilai true jika pada awalnya seluruh array bernilai false?
var ar : array[1..1000] of Boolean; i,j : integer; begin for i := 1 to 1000 do ar[i] := false; for i := 1 to 1000 do begin j := i; while(j <= 1000) do begin ar[j] := not(ar[j]); j := j + i; end; end; end.
Deskripsi Untuk Soal Nomor 35 dan 36
var isi : array[1..10] of integer = (-4,1,7,9,0,1,2,4,3,-1); function X(l, r, v : integer) : longint; var temp : integer; begin if(l = r) then X := isi[l] else begin temp := (l + r) div 2; if(isi[temp] > v) then begin X := X(l, temp, v); end else X := X(temp + 1, r, v); end; end;
35.
Lihat 2 jawaban →Jika dipanggil X(2,6,4), berapakah nilai kembaliannya?
36.
Jawab →Berapa kali fungsi X dipanggil pada pemanggilan X(1, 10, 0), termasuk pada saat dipanggil pertama kali?
Deskripsi Untuk Soal Nomor 37 dan 38
var daebak : array [0..2015] of char; w, x, y, z, i : integer; procedure saranghae(x : integer; len : integer); var i : integer; store : char; begin store := daebak[x]; for i := len-1 downto 0 do begin if (i = 0) then daebak[x+((i+1) mod len)] := store else daebak[x+((i+1) mod len)] := daebak[x+i]; end; end; procedure anyeong(arr_sz : integer; part_sz : integer); var i : integer; begin for i:= 0 to (arr_sz div part_sz)-1 do begin saranghae(i * part_sz, part_sz); end; end; procedure oppa(n : integer); var i : integer; begin for i := 0 to n-1 do begin if(i mod 4 = 0) then daebak[i] := 'T' else if(i mod 4 = 1) then daebak[i] := 'O' else if(i mod 4 = 2) then daebak[i] := 'K' else daebak[i] := 'I'; Sesi 2 : Bidang Informatika/Komputer Halaman 10 dari 14 OSP 2016 end; end; begin readln(w, x, y, z); oppa(w); for i := 1 to x do anyeong(y, z); for i := 0 to w-1 do begin if(i mod 4 = 0) and (i <> 0) then write(“ “); write(daebak[i]); end; writeln; end.
37.
Lihat 3 jawaban →Apa yang dihasilkan program di atas apabila yang diinputkan “16 2 12 4”?
38.
Jawab →Apa yang dihasilkan program di atas apabila yang diinputkan “16 4 10 5”?
Deskripsi Untuk Soal Nomor 39 dan 40
var
s, t: string;
x, l, r, k: byte;
temp: char;
begin
readln(s);
k := 0;
x := 0;
l := 1;
r := length(s);
t := '';
while (l <= r) do
begin
if (k mod 2) = 0 then
begin
temp := s[r];
r := r – 1;
end
else
begin
temp := s[l];
l := l + 1;
end;
k := k + 1;
// ord(c) adalah fungsi untuk mengubah
// karakter c menjadi nilai pada ASCII
// ord('A') = 65
// ord('B') = 66
// ...
// ord('Z') = 90
x := (x + ord(temp) - ord('A')) mod 26;
t := t + chr(x + ord('A'));
end;
writeln(t);
end.
39.
Lihat 2 jawaban →Apabila diberikan input berupa string “IXYBEJVCE”, tuliskan output dari program di atas.
40.
Jawab →Input apa yang harus diberikan agar output dari program di atas adalah “RJJJVDPII”?
Deskripsi Untuk Soal Nomor 41 dan 42
var Q : array[1..15] of integer = (1,5,2,3,4,6,2,7,3,4,6,0,-1,2,3); P : array[0..15] of integer; i, a, b,total : integer; begin P[0] := 0; for i := 1 to 15 do begin P[i] := P[i-1] + Q[i]; end; readln (a,b); total := 0; // baris-1 for i := a to b do begin // baris-2 total := total + Q[i]; // baris-3 end; // baris-4 writeln(total); end.
41.
Lihat 1 jawaban →Berapakah nilai total yang dikeluarkan sebagai output, apabila a = 6 dan b = 10?
42.
Jawab →Instruksi yang diberi komentar baris-1 sampai dengan baris-4 (lihat kode di atas) dapat digantikan dengan satu baris berisi instruksi: total := rumus;. Tuliskanlah rumus untuk mendapatkan hasil penjumlahan array Q dari indeks a sampai b (inklusif, 1 ? a ? b ? 15) dengan notasi dalam P, Q, a, dan b, misalnya anda menjawab: P[a*b] + Q[a-b].
Deskripsi Untuk Soal Nomor 43 dan 44
var isi : array[1..10] of integer; i : integer; procedure Whatsup(l, r : integer); var X : integer; begin X := isi[l]; isi[l] := isi[r]; isi[r] := X; end; procedure naoooon(l, r : integer); var ini : integer; kiri, kanan : integer; begin if(l < r) then begin kiri := l; kanan := r; ini := isi[(kiri + kanan) div 2]; while(kiri < kanan) do begin while(isi[kiri] > ini) do kiri := kiri + 1; while(isi[kanan] < ini) do kanan := kanan - 1; if(kiri < kanan) then Whatsup(kiri, kanan); end; naoooon(l, kanan); naoooon(kanan+1, r); end; end; begin isi[1] := 5; isi[2] := 10; isi[3] := 18; isi[4] := 1; isi[5] := 7; isi[6] := 9; isi[7] := 3; isi[8] := 8; isi[9] := 100; isi[10] := 29; naoooon(1,10); for i := 1 to 9 do write(isi[i], ' '); writeln(isi[10]); end.
43.
Lihat 1 jawaban →Tuliskan output program di atas.
44.
Jawab →Jika baris naoooon(1,10) diganti dengan naoooon(3, 6), tuliskanlah output program di atas.
45.
Lihat 2 jawaban →Tuliskanlah Input yang dapat mengeluarkan output berupa satu baris berisi angka-angka sebagai berikut:
1 2 3 4 5
untuk program sebagai berikut:
var ar : array[1..5] of integer; i : integer; procedure S(a,b : integer); var temp : integer; begin temp := ar[a]; ar[a] := ar[b]; ar[b] := temp; end; begin for i := 1 to 5 do read(ar[i]); S(3,4); S(4,1); S(5,2); S(5,1); for i := 1 to 4 do begin write(ar[i], ' '); end; writeln(ar[5]); end.
46.
Lihat 5 jawaban →PRIMA + PRIMA = PRIMA
Diberikan N buah bilangan prima berbeda P1, P2, P3, …, PN. Tentukan apakah ada sepasang bilangan prima Pi dan Pj dengan i ? j, yang apabila dijumlahkan akan menjadi bilangan prima juga.
Batasan :
- 2
N
100.000
- 1
Pk
500.000 untuk k dari 1 hingga N
- Pk dijamin bilangan prima untuk k dari 1 hingga N
Format Input :
Baris 1 : Sebuah bilangan N
Baris 2 : P1, P2, P3, …, PN Format Output : ADA / TIDAK ADA (sesuai deskripsi di atas)
Format Output :
ADA / TIDAK ADA (sesuai deskripsi di atas)
Sample input dan output :
|
5 |
ADA |
|
5 |
TIDAK ADA |
Keterangan :
Pada sample pertama, ada sepasang bilangan prima 11 and 2 yang apabila dijumlahkan adalah 13 yang juga merupakan bilangan prima.
Pada sample kedua, tidak ada sepasang bilangan prima yang apabila dijumlahkan menjadi bilangan prima lainnya.
47.
Lihat 6 jawaban →MENGHITUNG PERSEGI
Tahukah kamu bahwa grid berukuran 3x4 sebagai berikut memiliki 20 persegi (segi empat sama sisi)?

Diberikan N and M, tentukan banyaknya persegi yang terdapat pada grid berukuran NxM.
Batasan :
1 N,M
100.000
Format Input :
N M
Format Output :
Sebuah bilangan yang menyatakan banyaknya persegi yang terdapat pada grid berukuran NxM.
Sample input dan output :
| 3 4 | 20 |
| 4 3 | 20 |
| 1 10 | 10 |
| 5 5 | 55 |
48.
Lihat 7 jawaban →STRING PALINDROM
Terdapat suatu string dengan panjang N. Anda harus menentukan apakah string tersebut merupakan palindrom atau bukan. Palindrom adalah sebuah string yang jika dibaca dari kiri ke kanan akan sama dengan jika dibaca dari kanan ke kiri. Pada soal ini, String hanya berisi huruf alphabet kecil tanpa spasi. Jika string tersebut adalah sebuah palindrom, maka outputkan “PALINDROM” (tanpa tanda petik). Jika string tersebut bukan palindrom, maka outputkan “BUKAN PALINDROM” (tanpa tanda petik). Perhatikan contoh sebagai berikut:
| Input | Output |
| 4 abba |
PALINDROM |
| 4 abbb |
BUKAN PALINDROM |
| 1 a |
PALINDROM |
| 9 kasurrusak |
PALINDROM |
| 19 ospduaribuenambelas |
BUKAN PALINDROM |
Format Masukan :
Baris 1 : sebuah bilangan N
Baris 2 : sebuah string dengan panjang N. String dijamin memiliki panjang N.
Format Keluaran :
Output sesuai dengan program di atas.
Batasan:
1 N
100
Setiap karakter pada string merupakan huruf alphabet kecil.