Olimpiade Sains Kota (OSK) 2008 - Komputer
1.
Lihat 17 jawaban →Jika w, x, y dan z adalah ekspresi bilangan bulat, masing-masing persamaan berikut ini memiliki nilai yang sama, KECUALI
a. wx + wy + wz
b. 3w + x + y + z
c. (x + y + z)w
d. wx + w(y+z)
e. w(x + y) + wz
2.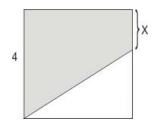
Lihat 10 jawaban →Perhatikan gambar bujur sangkar (persegi) berikut ini.

Panjang sisi-sisinya adalah 4. Harga x adalah bilangan positif yang tidak diketahui.Perbandingan(rasio) antara luas dari area yang diarsir dengan yang tidak adalah:
a. 2
b. 2x
c. (2 + x)/ 4
d. (4 – x)/8
e. (4 + x)/(4 – x)
3.
Lihat 9 jawaban →Jika Susan memiliki uang 5 ribu lebih banyak dari pada Tomi, dan Tomi memiliki 2 ribu lebih banyak dari pada Edi, bagaimanakan mereka harus saling berbagi untuk memastikan ketiganya memiliki jumlah uang yang sama ?
a. Susan harus memberikan 3 ribu kepada Edi dan seribu kepada Tomi.
b. Tomi harus memberikan 4 ribu kepada Susan dan Susan harus memberi 5 ribu kepada Edi.
c. Edi harus memberi Susan seribu dan Susan juga harus memberi Tomi seribu.
d. Susan harus menyerahkan kepada Edi 4 ribu dan Tom juga harus memberi Edi 5 ribu
e. Baik Susan maupun Edi harus memberi Tom 7 ribu.
4.
Lihat 3 jawaban →Seorang pelajar pergi ke sekolahnya, berangkat dari rumahnya ia berjalan kaki dengan kecepatan 5 km per jam. Tepat di pertengahan jarak antara rumah dan sekolahnya, ia bertemu teman karib sekolahnya yang sedang naik sepeda. Lalu ia segera dibonceng temannya hingga sampai disekolah. Kecepatan temannya memacu sepedanya adalah 15 km per jam. Berapakah kecepatan gabungan yang terjadi (jarak tempuh total dibagi total waktu)?
a. 7,5 km per jam
b. 10 km per jam
c. 12,5 km per jam
d. 13 km per jam
e. 20 km per jam
5.
Lihat 7 jawaban →Nainggolan 2 tahun lebih muda dari pada Marno yang usianya dua lipat usia dari Lisma. Jika umur ketiganya dijumlahkan, totalnya adalah 23 tahun, berapakah umur Marno ?
a. 5 tahun
b. 8 tahun
c. 9 tahun
d. 10 tahun
e. 12 tahun
6.
Lihat 3 jawaban →Herman diminta membantu ibunya untuk menempel lapisan kertas bermotif pada sebuah kotak karton yang memiliki dimensi panjang 16 cm, lebar 6 cm dan memiliki ketebalan 12 cm. Berapa cm2 kah kertas bermotif yang dia butuhkan untuk dapat melapisi kotak tersebut pada semua sisinya ?
a. 192
b. 360
c. 720
d. 900
e. 1440
7.
Lihat 3 jawaban →Huruf-huruf A,G,E,T,W,O,N masing-masing mewakili sebuah angka antara 1 sampai dengan 9 secara unik. AGE, TWO, NOT dan TO masing-masing merupakan bilangan kuadrat dari bilangan bulat, apakah hasil TWO+TO+TOO ?
a. NET
b. NAG
c. TON
d. TEN
e. ONE
8.
Lihat 2 jawaban →Pak Sanin mengisi sebuah bak penampungan air yang memiliki kapasitas 3750 meter kubik. Berapa lama waktu yang ia butuhkan untuk menyelesaikan pekerjaanya tersebut jika dia mengisi dengan menggunakan pompa air yang memiliki kapasitas 800 meter kubik per menit, dan tanpa sepengetahuannya ternyata pada bak penampungan air tersebut terdapat kebocoran yang cukup besar yang dapat mengakibatkan sejumlah 300 meter kubik permenit air terbuang sia-sia ?
a. 3 menit, 36 detik
b. 6 menit
c. 8 menit
d. 1875 menit
e. 7 menit, 30 detik
9.
Lihat 3 jawaban →Sejumlah 40% siswa SMA di Kabupaten M adalah laki-laki, 80% dari siswa laki-laki tersebut hadir menonton pertandingan sepakbola di lapangan, jika siswa laki-laki yang hadir tersebut berjumlah 1.152, berapakah jumlah total jumlah seluruh siswa SMA di Kabupaten M tersebut ?
a. 1440
b. 2880
c. 3600
d. 5400
e. 5760
10.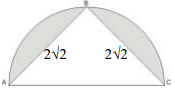
Lihat 2 jawaban →Perhatikan gambar berikut.

Pada gambar di atas, segitiga ABC terletak dalam sebuah setengah lingkaran; merujuk pada gambar diatas, berapakah luas daerah yang diarsir ?
a. 2π – 2
b. 2π – 4
c. 4π – 4
d. 8π – 4
e. 8π – 8
11.
Lihat 3 jawaban →Hartini berdiri di tengah suatu lapangan yang ditandai sebagai titik X, kemudian ia berturut-turut berjalan 10 meter ke arah timur, kemudian 20 meter ke arah utara, selanjutnya 10 meter ke timur lagi, lalu10 meter ke arah utara lagi, dan 10 meter ke arah timur lagi dan diakhiri dengan 10 meter ke arah utara sehingga mencapai posisi yang kita sebut sebagai titik Y. Jika suatu tali dipentangkan dari X ke Y (tidak yang menghalangi) berapakah panjang tali itu minimal?
a. 70 meter
b. 60 meter
c. 50 meter
d. 25 meter
e. 10 meter
12.
Lihat 1 jawaban →Karena hendak pergi ke luar negeri, Pak Dengklek menukarkan uangnya dengan dolar di sebuah tempat penukaran uang. Malangnya, karena salah membaca jumlah yang tertera di komputernya, pegawai penukaran uang tersebut terbalik dalam memberikan uang yang ditukarkan oleh Pak Dengklek. Ia memberikan 1 dolar untuk setiap sen jumlah seharusnya, dan sebaliknya memberikan 1 sen untuk tiap dolar jumlah seharusnya. Setelah menggunakan 50 sen yang diterimanya untuk membeli segelas minuman, Pak Dengklek baru menyadari bahwa uang yang ada padanya saat ini berjumlah 3 kali uang yang seharusnya ia terima dari tempat penukaran uang (Hal ini ia ketahui dari struk penukaran uang yang diterimanya, yang secara tak sengaja ia perhatikan sewaktu mengeluarkan dompetnya dari saku celananya). Berapakah uang yang seharusnya Pak Dengklek terima? (Catatan: 1 dolar = 100 sen.)
a. 23 dolar 67 sen
b. 18 dolar 56 sen
c. 32 dolar 45 sen
d. 49 dolar 30 sen
e. 105 dolar 67 sen
13.
Lihat 2 jawaban →Sebuah laci berisikan 4 buah kaus kaki berwarna hitam, 4 buah kaus kaki berwarna putih dan 4 buah kaus kaki berwarna merah. Jika kita tidak dapat melihat isi laci, berapakah jumlah kaus kaki minimum yang perlu diambil agar kita pasti mendapatkan setidaknya sepasang kaus kaki dengan warna yang sama?
a. 10
b. 6
c. 4
d. 8
e. 12
14.
Lihat 3 jawaban →Ada tiga buah kotak tertutup yang masing-masing berisikan 2 buah kelereng: kotak pertama berisikan dua kelereng putih, kotak kedua berisikan dua kelereng hitam, dan kotak ketiga berisikan satu kelereng putih dan satu kelereng hitam. Sewaktu akan diberi label, secara tidak sengaja urutan ketiga buah kotak itu tertukar sedemikian sehingga isi setiap kotak tidak sama dengan apa yang tertulis pada label kotak tersebut. Dengan asumsi kita hanya bisa mengetahui isi kotak dengan mengeluarkan kelereng satu per satu tanpa melihat ke dalam kotak, berapakah jumlah minimal seluruh kelereng yang harus dikeluarkan dari kotak-kotak tersebut agar kita dapat memastikan isi dari ketiga kotak tersebut?
a. 1
b. 2
c. 3
d. 4
e. 5
15.
Lihat 2 jawaban →Diketahui sebuah barisan bilangan yang dibentuk berdasarkan aturan:
-
Mulai dari sebuah bilangan dua digit;
-
Bilangan berikutnya adalah hasil perkalian dari digit-digit bilangan sebelumnya
- Berhenti ketika banyaknya digit = 1
Contoh: jika dimulai dari bilangan 88 maka berikutnya akan diperoleh 64, 24, dan 8. Barisan bilangan yang terbentuk (termasuk 88) memiliki panjang 4.
Dalam soal ini, temukanlah bilangan dua digit yang dengan aturan di atas dapat menghasilkan barisan bilangan dengan panjang 5 (termasuk bilangan itu sendiri). Berapakah bilangan tersebut?
a. 98
b. 77
c. 97
d. 88
e. 79
Deskripsi Untuk Soal Nomor 16 dan 18
Di sebuah sekolah terdapat 90 siswa yang sedang menempuh tahap persiapan ujian. Mereka diharuskan mengikuti setidaknya satu dari pelajaran-pelajaran tambahan berikut: Fisika, Bahasa Inggris, dan Sejarah. Dari keseluruhan siswa ini, terdapat 50 yang memilih Fisika, terdapat 60 yang memilih Bahasa Inggris, dan terdapat 55 yang memilih Sejarah. Tiga puluh siswa memilih Fisika dan Bahasa Inggris, sementara 10 siswa memilih Bahasa Inggris dan Sejarah tetapi tidak memilih Fisika. Dua puluh siswa memilih ketiga pelajaran tersebut.
16.
Lihat 5 jawaban →Berapakah banyak siswa yang memilih Fisika dan Sejarah, tetapi tidak memilih Bahasa Inggris?
a. 0
b. 45
c. 30
d. 15
e. 55
17.
Jawab →Berapa banyak siswa yang memilih setidaknya dua dari tiga pelajaran tersebut?
a. 55
b. 20
c. 10
d. 45
e. 35
18.
Jawab →Berapa banyak dari mereka yang hanya memilih satu pelajaran saja?
a. 55
b. 20
c. 10
d. 45
e. 35
Deskripsi Untuk Soal Nomor 19 dan 21
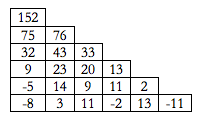
Andi senang bermain dengan angka. Ia menusun segitiga dari bilangan dengan aturan sebagai berikut. Di baris paling dasar sejumlah bilangan tertentu dituliskan. Pada baris di atasnya bilangan-bilangan diisikan namun bilangan pertama (terkiri) merupakan hasil penjumlahan bilangan pertama (terkiri) dan kedua dari baris tepat di bawahnya, bilangan kedua merupakan hasil penjumlahan bilangan kedua dan ketiga dari baris tepat di bawahnya, dan seterusnya. Tentu saja jika pada baris terbawah terdapat n bilangan maka pada baris di atasnya terdapat n-1 bilangan. Pada baris-baris berikut di atasnya, ia melakukan hal yang sama yaitu bilangan pertama adalah hasil penjumlahan 2 bilangan di baris tepat di bawahnya hingga tersisa baris puncak yang hanya berisi satu bilangan.
Contoh segitiga yang dihasilkan:
19.
Lihat 4 jawaban →Pada suatu segitiga yang dibuatnya diketahui di baris puncak terdapat bilangan -106, sementara di baris paling bawah terdapat bilangan lima bilangan yaitu: 24, 23, x, y, dan 12 (bilangan-bilangan x dan y tidak diketahui), jika (x – y) = 4 berapakah (x + y) ?
a. -23
b. 82
c. -46
d. 26
e. 12
20.
Jawab →Berapakah bilangan di puncak jika pada baris paling dasar terdapat 6 bilangan : 0, 10, 20, 30, 40, 50
a. 210
b. 1920
c. 960
d. 80
e. 100
21.
Jawab →Berapakah bilangan di puncak jika pada baris paling dasar terdapat 14 bilangan masing-masing berharga 1?
a. 512
b. 16384
c. 1960
d. 256
e. 8192
22.
Lihat 4 jawaban →Jika diketahui bahwa tepat dua pernyataan mengenai sebuah keluarga yang terdiri atas ayah, ibu, dan 2 orang anak kandung di bawah ini benar dan diketahui bahwa Ghani dan Arman berjenis kelamin laki-laki sementara Kiki dan Santi adalah perempuan. Diketahui sejumlah fakta berikut:
-
Ghani dan Santi memiliki hubungan darah
-
Arman lebih tua dari Ghani
-
Kiki lebih muda dari Arman
-
Kiki lebih tua dari Santi
- Posisi mereka masing-masing dalam keluarga adalah
a. Orang tua: Ghani dan Kiki, anak: Arman dan Santi
b. Orang tua: Arman dan Kiki, anak: Ghani dan Santi
c. Orang tua: Ghani dan Santi, anak: Arman dan Kiki
d. Orang tua: Arman dan Santi, anak: Ghani dan Kiki
e. Terdapat lebih dari satu kemungkinan jawaban yang benar
23.
Lihat 3 jawaban →Budi, Joni dan Sardi masing-masing berprofesi salah satu dari 3 pekerjaan ini: dokter, pengacara, dan guru. Sang guru, yang merupakan anak tunggal, memperoleh gaji paling sedikit. Sardi, yang merupakan kakak ipar Budi, bergaji lebih banyak dari sang pengacara. Apabila ketiga orang tersebut memiliki profesi yang berbeda-beda, dapat disimpulkan bahwa... (komentar: kakak ipar bisa juga anak tunggal kalau ia suami dari saudara Budi !!!)
a. Budi adalah seorang pengacara dan Joni adalah seorang guru
b. Sardi adalah seorang pengacara dan Budi adalah seorang guru
c. Sardi adalah seorang dokter dan Joni adalah seorang guru
d. Ada lebih dari satu jawaban yang benar
e. Tidak ada jawaban yang benar
24.
Lihat 2 jawaban →Bu Murni memiliki 3 anak: Andi, Budi dan Kardi. Ketika ditanya tentang usia ketiga anaknya, Bu Murni selalu menjawab dengan bahasa logika: ”Andi merupakan yang termuda, kecuali jika Budi merupakan anaknya yang termuda dan Kardi bukanlah anaknya yang termuda, maka Andi merupakan anaknya yang tertua”. Apabila ketiga anak Bu Murni itu tidak ada yang berusia sama, pernyataan logika yang pasti benar adalah...
a. Andi yang tertua
b. Jika ternyata Kardi yang termuda, maka Budi yang tertua
c. Budi yang termuda
d. Jika ternyata Budi bukan yang termuda, maka Kardi yang tertua
e. Jika ternyata Andi yang termuda, maka Budi yang tertua
Deskripsi Untuk Soal Nomor 25 dan 29
Delapan buah bola masing-masing bertuliskan angka berlainan mulai dari a, a+1, .. dan seterusnya hingga a+7. Bola-bola di tempatkan secara acak ke dalam 8 kotak yang masing-masing ditandai dengan huruf-huruf S, T, U V, W, X, Y dan Z. Setelah ditempatkan, diketahui bahwa:
-
W berisi bola dengan angka bernilai 4 lebih besar dari pada angka bola dalam Z dan bernilai 3 lebih kecil jika dibandingkan dengan angka bola dalam X
-
Sedangkan S berisi bola dengan angka bernilai nilai lebih besar dari pada angka bola di dalam T, dan lebih kecil dari pada angka bola di dalam X
- U berisi bola dengan angka yang merupakan nilai rata-rata dari angka bola dalam V dan X.
25.
Lihat 6 jawaban →Jika nilai terendah dari angka-angka tersebut adalah 8, berapakah angka bola dalam W ?
a. 10
b. 11
c. 12
d. 13
e. 15
26.
Jawab →Jika V lebih kecil dibandingkan W, manakah dari beberapan urutab berikut ini yang paling mungkin merupakan urutan dari angka-angka tersebut, dimulai dari angka yang terbesar di sebelah kiri ?
a. X, S, U, W, V, T, Y, Z
b. X, S, T, W, V, U, Y, Z
c. Z, S, T, W, U, V, Y, X
d. X, T, S, V, W, U, Z, Y
e. X, U, S, T, W, V, Y, Z
27.
Jawab →Manakah diantara beberapa pernyataan berikut yang bernilai benar ?
I. W tidak berisi bola angka yang terbesar dari rangkaian angka tersebut
II. Z bukanlah angka yang terbesar dari rangkaian angka tersebut
III. X bukanlah angka yang terbesar dari rangkaian angka tersebut
a. Hanya I yang benar
b. Hanya II yang benar
c. Hanya I dan II yang benar
d. Hanya I dan III yang benar
e. I, II dan III semuanya benar
28.
Jawab →Jika Y lebih besar 3 tingkat dari pada Z, periksalah pernyataan-pernyataan berikut ini.
I. W lebih besar dari U
II. S lebih besar dari W
III. Y lebih besar dari V
IV. Y lebih kecil dari T
Yang benar adalah:
a. Hanya I dan II yang benar
b. Hanya I dan III yang benar
c. Hanya I, II dan IV yang benar
d. Hanya II, III dan IV yang benar
e. Tidak ada yang benar
Deskripsi Untuk Soal Nomor 29 dan 31
Ada 5 rumah dalam 1 baris dari timur ke barat. Tiap rumah berbeda warnanya, dihuni 5 orang yang berbeda dengan peliharaan, makanan favorit, dan minuman favorit yang berbeda.
-
Ekas tinggal di rumah merah
-
Sandi memelihara anjing
-
Kopi diminum di rumah hijau
-
Udin senang minum teh
-
Rumah hijau berada di paling timur dan di samping rumah ungu
-
Yang suka nasi goreng memelihara siput
-
Yang tinggal di rumah kuning suka mie ayam
-
Susu diminum di rumah tengah
-
Nami tinggal di rumah paling barat
-
Yang suka soto tinggal disamping rumah yang memelihara rubah
-
Mie ayam dimakan di rumah yang memelihara kuda
-
Yang makan nasi padang suka minum jus jeruk
-
Joni suka makan tongseng
- Nami tinggal di sebelah rumah warna biru.
29.
Lihat 1 jawaban →Siapa yang suka minum air mineral?
a. Nami
b. Sandi
c. Udin
d. Joni
e. Ekas
30.
Jawab →Siapa yang memelihara Zebra?
a. Nami
b. Sandi
c. Udin
d. Joni
e. Ekas
31.
Jawab →Siapa yang senang minum jus jeruk?
a. Nami
b. Sandi
c. Udin
d. Joni
e. Ekas
Deskripsi Untuk Soal Nomor 32 dan 33
Perhatikan potongan algoritma berikut ini
j := 2;
for i := 0 to 10 do begin
if j > 0 then writeln(‘ok’);
j := 5 – (j*2);
end;32.
Lihat 5 jawaban →Berapa kalikah pencetakan keluaran „ok? dilakukan oleh potongan program itu?
a. 7
b. 3
c. 5
d. 6
e. 4
33.
Jawab →Berapakah harga j setelah keluar dari iterasi for tersebut?
a. 681
b. 600
c. -681
d. -702
e. -101
Deskripsi Untuk Soal Nomor 34 dan 35
Perhatikan potongan algoritma berikut ini
procedure Otakatik(j: integer; k: integer);
Var i: integer;
begin
for i := 1 to 10 do begin
if (j < 0)
then
if (k > 0)
then j := j + k
else k := -j + k
else
if (k < 0)
then j := -j - k
else k := j - k;
end;
writeln(j,’ ‘,k);
end;34.
Lihat 2 jawaban →Jika prosedur tsb dipanggil dengan perintah Otakatik(35,-10) berapakah harga yang dicetak perintah writeln(j,'',k)?
a. -25 25
b. 100 75
c. 0 -25
d. 25 -25
e. 5 -10
35.
Jawab →Pemanggilan manakah yang pada akhirnya variable j dan k kembali ke harga-harga semula (sebelum iterasi for dijalankan)?
a. Otakatik(2, 3)
b. Otakatik(-2,-3)
c. Otakatik(2, -3)
d. Otakatik(-2 , 3)
e. Otakatik(-3 , -2)
Deskripsi Untuk Soal Nomor 36 dan 37
Perhatikan potongan algoritma berikut.
for i := 1 to n do begin
case x of
1: x := (x + 22) mod 6;
2: x := x * 2;
3: dec(x);
4: x := 5 - x;
5: x := x shr 1 + 1;
else x := (x * 4) mod 5 + 1;
end;
writeln(x);
end;36.
Lihat 2 jawaban →Berapakah harga yang dicetak terakhir jika harga variable mula-mula x = 31 dan n = 1000?
a. 1
b. 2
c. 3
d. 4
e. 5
37.
Jawab →Berapa kalikah angka 5 muncul pada pencetakan yang dilakukan jika harga variable mula-mula x = 103 dan n = 10?
a. 11
b. 21
c. 13
d. 34
e. 20
Deskripsi Untuk Soal Nomor 38 dan 39
Perhatikan potongan algoritma berikut.
t:= 2;
while t <= n do begin
writeln(‘ok’);
t := t* 2 - 1;
end;38.
Lihat 2 jawaban →Berapa kalikah pencetakan 'ok' jika dijalankan dengan harga n = 100 ?
a. 3
b. 5
c. 7
d. 9
e. 11
39.
Jawab →Jika harga sembarang yang diberikan pada variable n sebagai N, maka banyaknya pencetakan 'ok' merupakan fungsi dari N manakah dari berikut ini?
Catatan: notasi ⌊f(N)⌋ menyatakan pembulatan ke bawah dari f(N).
a. N2
b. ⌊10log N⌋
c. 2N - 1
d. ⌊2 log N⌋
e. ⌊N/20 +2⌋
Deskripsi Untuk Soal Nomor 40 dan 41
Perhatikan potongan algoritma berikut.
var
a: array[1..8] of integer = (12, 30, 21, 8, 6, 9, 1, 7);
procedure zz(i: integer; j: integer);
var tmp: integer;
begin
tmp := a[i]; a[i] := a[j]; a[j] := tmp;
end;
var
h,k,val: integer;
begin
val := a[1];
h := 1;
for k := 2 to 8 do begin
if (a[k] < val) then begin
h := h + 1;
zz(h,k);
end;
end;
zz(1,h);
end.40.
Lihat 1 jawaban →Berapa kalikah zz() dijalankan dalam eksekusi algoritma tersebut?
a. 10
b. 5
c. 2
d. 6
e. 8
41.
Jawab →Berapakah isi array a setelah algoritma ini dijalankan?
a. (12, 30, 21, 8, 6, 9, 1, 7)
b. (1, 6, 7, 8, 9, 12, 21, 30)
c. (30, 21, 12, 9, 8, 7, 6, 1)
d. (1, 30, 6, 21, 7, 12, 8, 9)
e. (7, 8, 6, 9, 1, 12, 21, 30)
Deskripsi Untuk Soal Nomor 42 dan 43
Perhatikan fungsi berikut ini.
function A(i: integer; j: integer): integer;
begin
if (i >= 2) and (j >= 2) then A := A(i-1, A(i, j-1)+1)
else
if (i >=2) and (j = 1) then A := A(i-1, 2)
else
if (i = 1) and (j>= 1) then A := j
else
A := -1;
end;42.
Jawab →Pasangan manakah yang berharga sama?
a. A(3, 1) dengan A(2, 1)
b. A(3, 3) dengan A(2, 6)
c. A(4, 2) dengan A(3, 3)
d. A(3, 2 ) dengan A(2, 3)
e. A(4,2) dengan A(2, 4)
43.
Jawab →Berapakah A(4,7)?
a. 49
b. 509
c. 125
d. 253
e. 1021
Deskripsi Untuk Soal Nomor 44 dan 45
Perhatikan algoritma yang berisi sejumlah fungsi berikut ini:
function a(x:integer):integer;
begin
if (x>0) then
a:=b(x+1)
else
if (a<100) then
a:=b(-10)
else
a:=a(x-1);
end;
function b(y:integer):integer;
begin
if (y<0) then
b:=y*c(y)
else
b:=a(y-4);
end;
function c(z:integer):integer;
begin
if (c<0) then c:=1 else c:=-1;
end;44.
Jawab →Berapakah harga yang dihasilkan dalam pemanggilan writeln(a(128))?
a. 10
b. -10
c. 1
d. -1
e. 128
45.
Jawab →Manakah di antar nilai-nilai di bawah ini yang harus dimasukkan sebagai parameter dari pemanggilan fungsi a(x) agar nilai yang dikembalikan < 0:
a. 128
b. 2
c. -1
d. 86
e. 27
Deskripsi Untuk Soal Nomor 46 dan 47
Diberikan algoritma berikut ini:
procedure hitungsaja(n: integer; m: integer);
var k: integer;
begin
if (n < m) then begin
writeln(’hello’);
k := (m+n) div 2;
hitungsaja(n,k);
hitungsaja(k+1,m);
end else writeln(’hello’);
end;46.
Jawab →Pada pemanggilan hitungsaja(5,24) berapa baris keluaran (satu baris berisi berisi ?hello?) dicetak oleh algoritma tersebut?
a. 12
b. 32
c. 39
d. 44
e. 50
47.
Jawab →Pada pemanggilan hitungsaja(1,N) maka banyaknya baris keluaran yang dicetak oleh algoritma tersebut sebagai fungsi dari N adalah:
a. 1/2 N
b. N2
c. N(N+1)
d. 2N + 1
e. 2N – 1
Deskripsi Untuk Soal Nomor 48 dan 50
Diberikan kode program berikut ini:
var
zzz: integer;
junk: integer;
function ab(a, b: integer):integer;
begin
inc(zzz);
if (b<a) then
begin
ab:=a*b
end else
begin
ab:=ab(a+1, b-1);
end;
end;
function xyz(x, y, z: integer):integer;
var
t: integer;
begin
inc(zzz);
t:=ab(x, z);
xyz:=ab(t, y);
end;Soal Bidang Informatika Halaman 13 OSK 2008
{ program utama }
begin
writeln(xyz(10, 20, 30));
end.48.
Lihat 1 jawaban →Keluaran program adalah:
a. 7980
b. 6000
c. 9060
d. 4680
e. 1370
49.
Jawab →Manakah dari pemanggilan berikut yang akan menghasilkan nilai 2?
a. writeln(xyz(1, 1, 2));
b. writeln(xyz(2, 4, 2));
c. writeln(xyz(1, 3, 1));
d. Ada lebih dari satu jawaban benar
e. Tidak ada jawaban benar
50.
Jawab →Apabila program utama diganti menjadi:
begin
zzz:=0;
junk := xyz(10, 20, 30);
writeln(zzz);
end.maka, keluaran program adalah...
a. 15
b. 12
c. 13
d. 16
e. 14