Olimpiade Sains Provinsi (OSP) 2018 - Komputer
1.
Lihat 14 jawaban →Jika sedang tidak marah, Pak Dengklek biasanya suka bernyanyi sepanjang hari. Jika sebaliknya, dia tidur-tiduran sepanjang hari di kamarnya. Tetapi dia juga akan tidur-tiduran di kamarnya jika dalam keadaan sakit. Gara-gara tiduran, dia tidak bisa memberikan makan bebek-bebeknya sehingga makanan bebeknya akan tersisa. Sore ini terlihat makanan bebeknya tidak tersisa. Apakah Pak Dengklek sedang marah?
2.
Lihat 5 jawaban →Diberikan sembilan variabel boolean X1 s.d. X9 . Dari kesembilan variabel tersebut, dibuat beberapa kalimat boolean, yaitu:
- X2 xor (~X1 )
- (~X5 ) xor X6
- X5 xor X4
- (~X3 ) xor (~X4 )
- X3 xor (~X5 )
- X7 xor (~X8 )
- (~X9 ) xor X9
- X6 xor X3
Ada berapa kemungkinan konfigurasi X1 s.d. X9 yang membuat setidaknya ada satu kalimat bernilai FALSE? Dua konfigurasi dikatakan berbeda apabila di antara dua konfigurasi tersebut terdapat setidaknya satu Xi (1 <= i <= 9) yang bernilai beda. (Catatan: A xor B akan bernilai TRUE jika nilai A dan B tidak sama.)
3.
Lihat 5 jawaban →Pak Blangkon beternak dua jenis ayam yaitu ayam kampung dan ayam ras. Di halaman belakang rumahnya ada 35 ekor ayam jantan. Di antaranya, 15 ekor adalah ayam kampung, 19 ekor berjengger panjang, dan 25 ekor berkokok keras. Ayam kampung jantan yang berkokok keras ada sebanyak 12 ekor, ayam kampung jantan berjengger panjang ada sebanyak 7 ekor, sedangkan ayam jantan yang berjengger panjang dan berkokok keras ada sebanyak 9 ekor. Berapakah jumlah ayam kampung jantan yang berjengger panjang dan berkokok keras yang dimiliki Pak Blangkon?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
4.
Lihat 2 jawaban →Pak Dengklek memiliki 10 ekor bebek di mana jumlah bebek betina dan jantan sama banyaknya. Dia ingin memasangkan tiap bebek betina dengan bebek jantan. Pak Dengklek memberi aturan bahwa setiap bebek jantan dan bebek betina yang dipasangkan akan dihitung selisih berat badannya. Selisih berat badan setiap pasangan kemudian akan dikalikan. Diketahui bahwa berat bebek betina berturut-turut adalah 1, 2, 3, 4, dan 5. Sedangkan berat bebek jantan beratnya berturut-turut adalah 5, 4, 3, 2, dan 1. Berapa banyak konfigurasi lima pasangan bebek yang hasil perkalian selisih-selisihnya genap bukan nol?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
5.
Lihat 3 jawaban →Misalkan A dan B berturut-turut menyatakan bilangan terbesar dan bilangan terkecil di antara semua bilangan 5-digit (digit pertama tidak boleh nol), di mana ketika digit-digitnya dijumlahkan akan bernilai 9. Berapakah digit terakhir dari 3(A-B)?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
6.
Lihat 3 jawaban →Pak Dengklek baru saja membuka tabungan di Bank TOKI. Supaya ATMnya aman maka dia harus membuat 4digit PIN sedemikian sehingga jika PIN-nya dikali dengan angka 4 maka hasilnya adalah PIN dengan urutan digit terbalik. Tentukan PIN yang dimiliki oleh Pak Dengklek?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
7.
Lihat 5 jawaban →Kotak-kotak pada gambar berikut merepresentasikan ruangan-ruangan. Sebuah ruangan bertetangga dengan empat ruangan di sebelah kiri, kanan, atas dan bawahnya kecuali ruangan yang letaknya di pinggir atau di pojok. Di setiap ruangan terdapat sebuah lampu dan sebuah saklar yang terhubung ke lampu tersebut dan lampu di ruangan tetangganya. Jika sebuah saklar ditekan, maka lampu yang terhubung dengannya akan berubah dari nyala menjadi padam atau sebalikya. Dalam gambar di bawah ini, kotak berwarna putih menyatakan ruangan dengan lampu yang menyala, sedangkan kotak berwarna hitam menyatakan ruangan dengan lampu yang padam.

Berapa kali paling sedikit penekanan saklar yang diperlukan untuk menghidupkan seluruh lampu jika penekanan dilakukan satu per satu (tidak ada yang bersamaan)?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
8.
Lihat 5 jawaban →Pak Dengklek sedang bermain menyusun bentuk segitiga dengan menggunakan batang korek api. Contoh untuk menyusun dua bentuk segitiga diperlukan minimal 5 batang korek api. Syarat yang perlu diperhatikan adalah bahwa setiap batang korek api yang dipakai harus utuh tidak boleh terpotong, serta satu segitiga dihitung ada jika sisi-sisinya dibentuk dari satu batang korek api
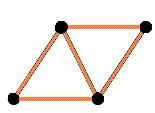
Berapakah batang korek api minimal yang diperlukan untuk membentuk dua puluh segitiga dengan syarat seperti disebutkan di atas?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
9.
Lihat 3 jawaban →Diberikan peta rumah-rumah di kota Pak Dengklek tinggal seperti berikut:
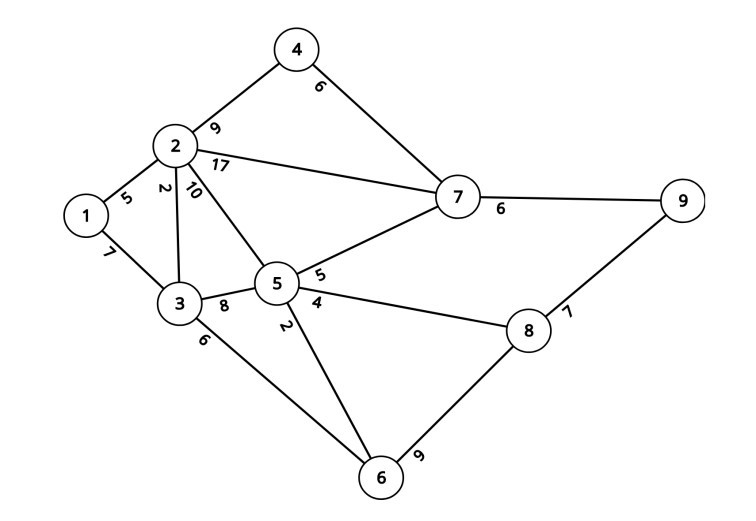
Setiap rumah memiliki nomor dari 1 sampai 9. Dua buah rumah dihubungkan dengan sebuah jalan yang memiliki panjang tertentu. Pak Dengklek sedang berada di rumah no. 1 dan ingin berkunjung ke rumah no. 9. Ada berapa banyak rute berbeda yang dapat Pak Dengklek tempuh dengan total lintasan sependek mungkin? Dua buah rute dikatakan berbeda jika terdapat setidaknya satu jalan berbeda yang dipilih dari satu rute, tetapi tidak pada rute lainnya.
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
10.
Lihat 3 jawaban →Aang, Budi, Cici, Dika dan Eno bermain ayam-bebek. Setiap anak menjadi ayam atau bebek, tetapi tidak keduaduanya. Ayam selalu jujur dan bebek selalu berdusta. Aang berkata bahwa Budi adalah ayam. Cici berkata bahwaDika adalah bebek. Eno berkata Aang bukan bebek. Budi berkata Cici bukan ayam. Dika berkata bahwa Eno dan Aang adalah binatang yang berbeda. Ada berapa anak yang menjadi bebek dalam permainan ini?
Jawaban: ……………. {tuliskan jawaban dalam bentuk satu kata}
11.
Lihat 3 jawaban →Terdapat sebuah daftar yang memuat 2017 pernyataan sebagai berikut:
Pernyataan nomor 1: Terdapat tepat 1 pernyataan dalam daftar ini yang salah.
Pernyataan nomor 2: Terdapat tepat 2 pernyataan dalam daftar ini yang salah. Pernyataan nomor 3: Terdapat tepat 3 pernyataan dalam daftar ini yang salah.
...
Pernyataan nomor 2016: Terdapat tepat 2016 pernyataan dalam daftar ini yang salah.
Pernyataan nomor 2017: Terdapat tepat 2017 pernyataan dalam daftar ini yang salah.
Pernyataan nomor berapakah yang benar jika ternyata hanya ada satu yang benar?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
12.
Lihat 5 jawaban →Iwan selalu berbohong pada hari Senin, Selasa, Rabu dan berkata jujur pada hari-hari lainnya. Di lain pihak Budi selalu berbohong pada hari Kamis, Jumat, Sabtu dan berkata jujur pada hari-hari lainnya. Pada suatu hari terjadi percakapan berikut:
Iwan: “Kemarin saya berbohong”
Budi: “Saya juga”
Pada hari apa percakapan tersebut terjadi?
Jawaban: ……………. {tuliskan jawaban dalam bentuk satu kata}
13.
Lihat 4 jawaban →Saat belanja di sebuah pusat perbelanjaan, Pak Dengklek berencana membeli beberapa permen untuk 5 keponakannya. Dalam kotak terdapat 17 permen dengan 4 rasa, yaitu 2 permen rasa anggur, 3 permen rasa jeruk, 7 permen rasa mangga, dan 5 permen rasa strawberry. Pak Dengklek ingin membelikan permen untuk kelima keponakannya dengan rasa yang sama. Berapakah jumlah permen paling sedikit yang harus dibeli agar selalu diperoleh 5 permen dengan rasa yang sama?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
14.
Lihat 2 jawaban →Pak Dengklek sedang bermain dengan 10 buah kartu. Setiap kartu tersebut diberi nomor dari 1 hingga 10. Pada awal permainan, kartu tersebut disusun secara terurut sehingga kartu nomor 1 berada di paling atas dan kartu nomor 10 berada di paling bawah. Satu langkah dilakukan dengan mengambil satu kartu teratas dan diletakkan di tumpukan paling bawah. Satu putaran adalah melakukan X langkah, yang mana untuk putaran ke-i (dimulai dari 1), X menyatakan bilangan prima ke-i. Setelah melakukan satu putaran, Pak Dengklek akan membuang kartu teratas pada tumpukan. Pak Dengklek melakukan hal ini sampai tersisa 1 kartu. Berapakah nilai pada kartu yang tersisa?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
15.
Lihat 2 jawaban →Pak Dengklek memiliki dua buah bilangan bulat positif, tetapi Ia lupa berapa nilai dari kedua bilangan tersebut. Namun, Ia ingat bahwa jumlah dari kedua bilangan tersebut adalah 105. Kemudian FPB dan KPK dari kedua bilangan tersebut secara berturut-turut adalah 15 dan 150. Berapakah selisih dari kedua bilangan tersebut?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
16.
Lihat 3 jawaban →Pada bulan April, desa TOKI Jaya akan menjadi tuan rumah pelaksanakan turnamen sepakbola antar desa senegara TOKI. Diperkirakan akan ada banyak orang yang datang ke desa untuk menyaksikan pertandingan. Masalahnya, para penonton pasti datang menggunakan kendaraan pribadi maupun bus dan membutuhkan tempat parkir. Di desa TOKI terdapat area kosong dengan luas sebesar 360 m2 yang bisa dimanfaatkan untuk area parkir. Pak Blangkon ditugaskan untuk mengatur perparkiran. Luas rata-rata sebuah mobil 6 m2 dan luas rata-rata bus 24 m2. Daerah parkir tersebut dapat memuat paling banyak 30 kendaraan roda empat (mobil dan bus). Jika tarif parkir mobil Rp2.000,00 dan tarif parkir bus Rp5.000,00 maka pendapatan terbesar yang dapat diperoleh adalah?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
17.
Lihat 2 jawaban →Untuk mengembangkan usaha peternakannya, Pak Dengklek juga akan memelihara ayam disamping bebek-bebeknya. Setiap hari, Pak Dengklek akan menambah jumlah hewan ternaknya dengan membeli ke toko bebek atau toko ayam secara berselang-seling. Sebagai contoh, apabila kemarin ia pergi ke toko bebek maka hari ini ia akan pergi ke toko ayam. Pak Dengklek juga memiliki sebuah aturan pembelian:
- apabila kemarin ia membeli x ekor bebek, maka hari ini ia akan membeli 2x ekor ayam
- apabila kemarin ia membeli y ekor ayam, maka hari ini ia akan membeli 3y ekor bebek
Tentukan hewan ke-1000 yang Pak Dengklek beli jika hari pertama ia membeli seekor bebek!
Jawaban: ……………. {tuliskan jawaban dalam bentuk satu kata}
Deskripsi Untuk Soal Nomor 18 dan 19
Terdapat dua binatang purba pada tahun 0 Masehi. Satu binatang akan melahirkan tiga anak sekaligus setelah satu tahun dan tidak akan bisa beranak lagi setelah itu. Sehingga akan ada 8 binatang pada tahun 1 Masehi, 26 binatang pada tahun 2 Masehi dst.
18.
Lihat 3 jawaban →Berapa banyak binatang purba pada tahun ke 5 Masehi?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
19.
Jawab →Berapa banyak binatang purba pada tahun 2018 Masehi (jawaban dimodulo 2017)?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
Deskripsi Untuk Soal Nomor 20 dan 21
Pak Dengklek mempunyai suatu lantai berukuran N * N petak, yang mana nilai N selalu genap. Terdapat ((N * N / 2) - 1) tegel berukuran 1 x 2 untuk dipasangkan ke lantai tersebut. Pak Dengklek ingin memilih dua petak pada lantai yang tidak akan dipasang tegel untuk dicat dengan warna merah, dan menutupi petak sisanya dengan tegel-tegel tersebut. Berikut adalah beberapa contoh dari pemasangan tegel pada N = 4, dengan banyaknya tegel adalah 7.
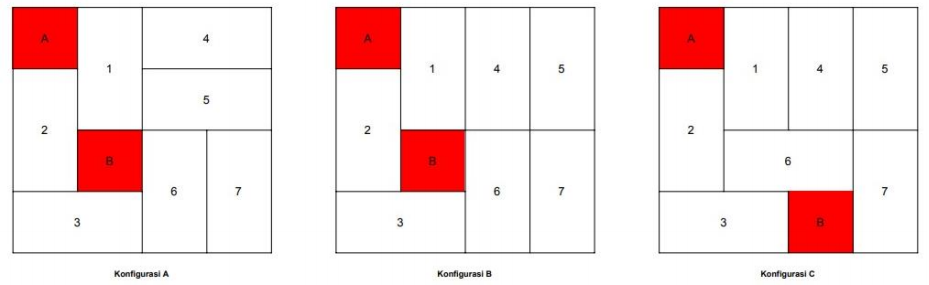
Pada ketiga gambar diatas, terdapat 7 tegel yang dinomori dari 1 - 7, dan petak yang tidak dipasang tegel ditandai dengan warna merah. Suatu konfigurasi disebut menarik apabila terdapat minimal satu cara untuk meletakkan seluruh tegel tanpa keluar dari lantai maupun kedua petak berwarna merah. Pada gambar diatas, konfigurasi A, B, maupun C merupakan konfigurasi yang menarik.
Suatu konfigurasi menarik X disebut berbeda dengan suatu konfigurasi menarik Y apabila posisi petak berwarna merah berbeda. Pada gambar diatas, konfigurasi A sama dengan konfigurasi B, akan tetapi konfigurasi C berbeda dengan konfigurasi A maupun B.
20.
Lihat 3 jawaban →Apabila diketahui N = 2, berapa banyak konfigurasi menarik yang berbeda?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
21.
Jawab →Apabila diketahui N = 10, berapa banyak konfigurasi menarik yang berbeda?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
22.
Lihat 3 jawaban →Pak Dengklek menyatakan suatu bilangan disebut bagus apabila bilangan tersebut habis dibagi 3. Pak Dengklek menyatakan suatu bilangan disebut cantik apabila bilangan tersebut memiliki banyak faktornya ganjil. Jika Pak Dengklek memiliki suatu bilangan X, berapakah minimum nilai N supaya banyaknya bilangan dari [1..N] yang bagus atau cantik adalah lebih besar dari atau sama dengan X apabila diberikan nilai X=100?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
23.
Lihat 4 jawaban →Pak Dengklek sedang bermain Tebak Angka bersama Pak Ganesh. Terdapat 100 bilangan bulat. Pak Dengklek memilih sebuah bilangan di antara 1 sampai 100, lalu Pak Ganesh berusaha menebak bilangan yang dipilih Pak Dengklek. Setiap putarannya, Pak Ganesh dapat menyebutkan sebuah bilangan, dan Pak Dengklek dapat memberikan umpan balik "Kurang Dari", "Sama Dengan", dan "Lebih Dari" sesuai dengan bilangan yang dipilih. Permainan berhenti apabila Pak Ganesh berhasil menebak bilangan yang dipilih Pak Dengklek, yaitu saat Pak Dengklek memberikan umpan balik "Sama Dengan". Paling sedikit berapa kali Pak Ganesh menyebut angka tebakan sehingga dijamin bahwa Pak Ganesh dapat menebak bilangan yang dipilih Pak Dengklek dengan benar untuk setiap kasus?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
Deskripsi Untuk Soal Nomor 24 dan 25
Terdapat sebuah petak berbentuk persegi panjang yang memiliki 4 baris dan tak hingga kolom, setiap lokasi akan didefinisikan dengan (baris, kolom). Pak Dengklek (D) sedang berdiri di pojok kiri atas (1,1), dan Pak Ganesh (G) sedang berdiri di pojok kiri bawah (4,1) seperti pada gambar di bawah ini:
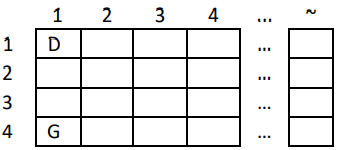
Mereka berdua secara bersama-sama dapat melangkah secara diagonal ke kolom sebelah kanan mereka, dengan syarat mereka berdua tetap berada dalam petak tersebut dan tidak saling bertabrakan. Mereka melanjutkan proses tersebut hingga tiba di kolom 3.
24.
Lihat 4 jawaban →Berapa banyak cara berbeda untuk mereka berdua berjalan menuju ke kolom 5?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
25.
Jawab →Berapa banyak cara berbeda untuk mereka berdua berjalan menuju ke kolom 1357? Jawaban dalam modulo 7.
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
26.
Lihat 3 jawaban →Diberikan sebuah array berisi [3, 9, 1, 7, 2, 5], satu langkah didefinisikan sebagai pemilihan dua buah angka, menghapus salah satunya, dan menambah nilai absolut dari selisih kedua angka tersebut pada angka yang tidak dihapus. Sebagai contoh anda mengambil dua buah angka A dan B, kemudian menghapus angka A, dan menambahkan selisih absolut (A-B) ke angka B. Anda dapat menjalankan langkah tersebut sampai terdapat hanya tersisa 1 angka. Berapakah nilai terbesar yang bisa anda dapatkan?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
27.
Lihat 5 jawaban →Pak Dengklek menggulirkan sebuah dadu sepanjang jalan tanpa pengeseran. Untuk memindahkan dadu dari satu petak ke petak berikutnya, Pak Dengklek memutar dadu sepanjang pinggir yang ada di perbatasan antara dua petak. Dia melakukannya 7 kali sampai dadu mencapai petak berisi bulatan putih di sebelah kanan.
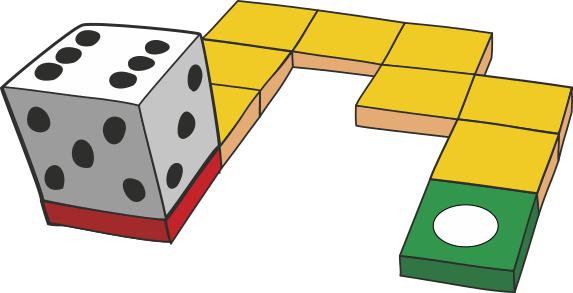
Perhatikan bahwa banyaknya titik di sisi kebalikan sebuah dadu selalu 7 (1 berlawanan dengan 6; 2 berlawanan dengan 5; 3 berlawanan dengan 4). Pada mulanya, sisi dengan 1 titik (berlawanan dengan sisi 6) ada di dasar dadu, seperti ditunjukkan pada gambar. Setelah memutar dadu sekali ke petak kedua, sisi dengan 2 titik (berlawanan dengan 5) akan berada di dasar dadu. Sisi dadu dengan berapa titik ada di dasar dadu saat dadu mencapai petak hijau di ujung?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
Deskripsi Untuk Soal Nomor 28 dan 29
Dalam sebuah pertandingan olahraga, Budi diberikan kesempatan untuk memilih urutan pemain yang harus dilawannya. Asumsikan ada N orang lawan yang masing-masing memiliki tingkat kemahiran Ai. Setelah Budi berhasil mengalahkan pemain ke-i, tingkat kemahirannya akan bertambah sebanyak Bi yang akan digunakan untuk melawan pemain selanjutnya. Perlu diingat bahwa Budi hanya bisa mengalahkan pemain dengan tingkat kemahiran yang lebih rendah atau sama dengan dirinya sendiri. Jika Budi memiliki tingkat kemahiran awal M, anda diminta untuk menentukan urutan pemain manakah yang harus dilawan Budi secara berurutan sampai dia tidak bisa lagi mengalahkan lawannya sehingga Budi mendapatkan tingkat kemahiran yang maksimal.
28.
Lihat 3 jawaban →Jika diketahui Budi saat ini memiliki tingkat kemahiran 2 dan akan melawan 4 orang lainnya dengan nilai Ai dan Bi sebagai berikut:

Berapakah tingkat kemahiran maksimal yang akan diperoleh Budi?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
29.
Jawab →Jika diketahui lawan-lawan Budi adalah sebagai berikut:

Berapakah tingkat kemahiran minimum yang harus dimiliki Budi supaya bisa mengalahkan semua lawan-lawannya?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
Deskripsi Untuk Soal Nomor 30 dan 31
Untuk menghilangkan penat, Pak Blangkon sering sekali jalan-jalan ke pekarangan di belakang rumahnya. Pekarangannya berukuran 7x8 petak yang di dalamnya terdapat N buah pohon. Saat berada di posisi tertentu Pak Blangkon menyadari bahwa hanya beberapa pohon saja yang bisa terlihat pada delapan arah mata angin, karena pohon tertentu berada tepat di belakang pohon lainnya saat pandangan tertuju pada arah tertentu. Jika dilihat dari atas dalam koordinat dua dimensi, Pak Blangkon ada di posisi B sedangkan pohon-pohonnya ada di posisi P. Seperti contoh pada gambar di bawah ini.
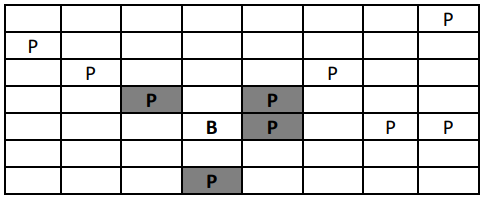
Pada gambar di atas, dari 10 pohon hanya 4 pohon yang bisa dilihat secara langsung oleh Pak Blangkon pada delapan arah mata angin, sedangkan pohon-pohon lainnya terhalang oleh pohon di depannya.
30.
Lihat 4 jawaban →Jika susunan pohon dalam pekarangan Pak Blangkon adalah sebagai berikut:
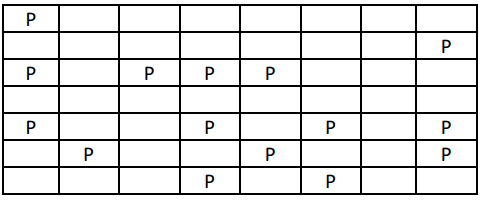
Ada berapa kemungkinan posisi Pak Blangkon harus berdiri supaya jumlah pohon yang bisa dilihatnya semaksimal mungkin?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
31.
Jawab →Diketahui susunan pohon dalam pekarangan Pak Blangkon adalah sebagai berikut:
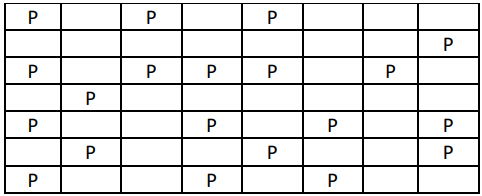
Pak Dengklek bertamu ke rumah Pak Blangkon dan diajak berkeliling di pekarangannya. Karena Pak Dengklek benci pohon, ada berapa kemungkinan posisi Pak Blangkon harus berdiri bersama Pak Dengklek supaya jumlah pohon yang bisa dilihat seminimal mungkin?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
32.
Lihat 1 jawaban →Pak Dengklek memiliki 10 pot bunga dengan tiap – tiap pot bunga ditanami jenis bunga yang unik. Pot-pot bunga tersebut diletakkan sejajar dalam satu baris. Suatu hari, Pak Dengklek memutuskan untuk mengubah susunan pot-pot bunga tersebut dengan syarat tidak boleh ada sebarang dua pot bunga yang bersebelahan pada susunan sebelumnya akan tetap bersebelahan pada susunan yang baru. Berdasarkan syarat tersebut, berapa banyak susunan pot-pot bunga baru dapat dibuat oleh Pak Dengklek.
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
33.
Lihat 3 jawaban →Terdapat 16 koin yang berjejer dalam satu baris di atas meja dengan konfigurasi awal sebagai berikut. (A berarti Angka, G berarti Gambar)
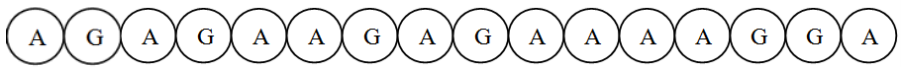
Pak Dengklek memainkan sebuah permainan. Dia akan memilih dua buah koin yang tepat saling bersebelahan, kemudian membalik sisi keduanya, gambar menjadi angka, serta angka menjadi gambar. Proses ini dianggap sebagai satu langkah. Langkah tersebut kemudian akan terus diulang hingga semua koin menunjukkan sisi gambar. Berapa kali langkah minimal yang harus dilakukan Pak Dengklek agar semua koin menunjukkan sisi gambar?
Jawaban: ……………. {tuliskan jawaban dalam bentuk angka saja}
34.
Lihat 4 jawaban →Diberikan program di bawah ini. Berapakah output dari program tersebut? {tuliskan jawaban sesuai dengan output yang dihasilkan}
var
rumah: array[1..25] of integer;
procedure buat(x, y:integer);
begin
rumah[x] := rumah[x] + 1;
rumah[y+1] := rumah[y + 1] -1;
end;
function hitung():integer;
var
i, tmp, pintu, jendela: integer;
begin
tmp := 0; pintu := 0; jendela := 0;
for i := 1 to 25 do
begin
tmp := tmp + rumah[i];
if tmp > pintu then
begin
pintu := tmp;
jendela := i;
end;
end;
hitung := jendela;
end;
begin
buat(4, 8);
buat(3, 6);
buat(10, 15);
buat(14, 20);
writeln(hitung());
end.
35.
Lihat 2 jawaban →
Diberikan fungsi seperti di bawah ini. Berapakah nilai dari toki(12, 8, 6)? {tuliskan jawaban sesuai dengan output yang dihasilkan}
function indra(ini, itu : longint): longint;
begin
if (itu = 0) or (ini = itu) then
indra := 1
else
indra := indra(ini - 1, itu - 1) + indra(ini - 1, itu);
end;
function toki(haha, hihi, huhu : longint): longint;
var
hehe, hoho : longint;
begin
hoho := 0;
for hehe := 0 to huhu do
hoho := hoho + indra(haha, hehe) * indra(hihi, huhu - hehe);
toki := hoho;
end;
36.
Lihat 3 jawaban →Diberikan program seperti di bawah ini. Berapakah output dari program tersebut? {tuliskan jawaban sesuai dengan output yang dihasilkan}
var i,j,k,sum:integer;
begin
sum:=0;
for i:= 1 to 10 do
begin
j:=0; k:=i;
while (k>0) do
begin
sum:=sum+j+k;
j:=j+1; k:=k-1;
end;
end;
writeln(sum);
end.
37.
Lihat 1 jawaban →Diberikan program di bawah ini. Apa output dari program tersebut? {tuliskan jawaban sesuai dengan output yang dihasilkan}
var a :array[1..10] of integer; b :integer; i :integer; sum :integer; procedure kwak(x:integer); begin b :=b+1; a[b] :=x; end; procedure kwek; var x :integer; begin a[b] :=x; b :=b-1; end; procedure kwik; begin for i :=1 to b-1 do begin a[i] :=a[i+1]; end; b :=b-1; end; procedure kwok; begin sum :=0; for i:=1 to b do begin m := sum + a[i]; end; writeln(sum); end; begin b:=0; kwak(8); kwak(7); kwek; kwak(18); kwak(28); kwak(35); kwek; kwik; kwok; end.
38.
Lihat 2 jawaban →Diberikan fungsi seperti di bawah ini. Berapakah nilai dari f(8, 4)? {tuliskan jawaban sesuai dengan output yang
dihasilkan}
var e : array[1..10] of integer = (6, 7, 4, 5, -1, 4, -1, 3, 1, 9);
function f(a, b: integer): integer;
begin
if a = b then
f := 1
else if e[a] = -1 then
f := 0
else f := 2 * f(e[a], b);
end;
39.
Lihat 2 jawaban →Diberikan procedure seperti di bawah ini. Apakah output dari program tersebut jika dipanggil lacak(9,6,7,4)? {tuliskan jawaban sesuai dengan output yang dihasilkan}
procedure lacak(a,b,c,d:integer);
begin
if (a>b) and (c>d) then
begin
if (a>d) or (c<d) then
begin
if (b<d) then
writeln(a)
else
writeln(b);
end else
begin
writeln(c);
end;
end else
begin
if (a=d) or (c=d) then
begin
if (b<c) then
writeln(b)
else
writeln(c);
end else
writeln(d);
end;
end;
40.
Lihat 2 jawaban →Diberikan program di bawah ini. Tuliskan output dari program tersebut. {tuliskan jawaban sesuai dengan
output yang dihasilkan}
function movpush(a, b :integer):integer;
var x: integer;
begin
while(b <> 0) do
begin
x := a and b;
x := x shl 1;
a := a xor b;
b := x;
end;
movpush := a
end;
begin
writeln(movpush(movpush(300, 510), movpush(0, 110)));
end.
41.
Lihat 10 jawaban →SERTIFIKAT
Pak Dengklek berencana memberikan penghargaan kepada siswanya yang memilik nilai terbaik dalam kelas yang diajarkannya. Untuk menentukan siapa saja yang akan mendapatkan sertifikat, pertama Pak Dengklek menentukan nilai maksimal dari siswa dalam kelas. Setiap siswa yang memiliki nilai sama dengan nilai maksimal dalam kelas maka akan mendapatkan penghargaan berupa sertifikat. Jika diketahui N nilai siswa, bantulah Pak Dengklek untuk menentukan berapa banyak sertifikat yang harus di cetak.
Format Masukan:
Masukan terdiri dari 2 baris. Baris pertama berisi bilangan bulat N. Bari kedua berisi N buah bilangan Ai, di mana Ai menyatakan nilai dari siswa ke-i yang dipisahkan dengan spasi.
Format Keluaran:
Banyaknya sertifikat yang harus dicetak oleh Pak Dengklek.
Batasan:
- 2 <= N <= 100.000
- 1 <= Ai <= 100
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|
5 87 100 89 100 90 |
2 |
|
8 87 99 89 99 90 90 99 70 |
3 |
42.
Lihat 3 jawaban →OLEH-OLEH BATU GIOK
Pak Blangkon baru saja kembali ke Negeri TOKI. Karena kangen dengan Pak Dengklek, diapun berencana memberikan oleh-oleh berupa N buah batu giok. Setiap giok ke-i memiliki berat Bi. Pak Blangkon tahu bahwa Pak Dengklek hanya mau menerima sekumpulan batu giok jika memiliki berat yang berbeda-beda dan faktor perseketuan terbesar berat dari sekumpulan batu giok tersebut bernilai sama dengan 1.
Diberikan sekumpulan N batu giok dengan berat masing-masing Bi (1 <= i <= N). Anda diminta untuk membuat sebuah program yang menentukan apakah sekumpulan batu giok layak sebagai hadiah sesuai dengan keinginan Pak Dengklek.
Format Masukan:
Masukan terdiri dari 2 baris. Baris pertama berisi bilangan bulat N. Baris kedua berisi N buah bilangan Bi yang menyatakan berat giok ke-i yang dipisahkan dengan spasi.
Format Keluaran:
Tuliskan LAYAK jika berat sekumpulan N batu giok tersebut sesuai dengan keinginan Pak Dengklek. Sebaliknya tuliskan TIDAK LAYAK.
Batasan:
- 2 <= N <= 10.000
- 2 <= Bi <= 100.000
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|
2 10 15 |
TIDAK LAYAK |
|
3 50 625 75 |
TIDAK LAYAK |
|
3 7 9 11 |
LAYAK |
|
5 2 3 7 11 17 |
LAYAK |
43.
Lihat 2 jawaban →ANGKA SUBSEKUENS
Pak Dengklek memiliki array yang berisi N elemen, setiap elemen berada diantara 0 sampai 9 (inklusif). Pak Dengklek ingin mencari suatu subsekuens valid terpanjang dari array tersebut. Subsekuens dari suatu array adalah sekuens yang dapat diperoleh dengan menghapus beberapa elemen array tanpa mengubah urutan dari array tersebut. Sebagai contoh, array {1, 3, 3, 6, 7} memiliki subsekuens {1, 3, 6}, {1, 6, 7}, tetapi bukan {1, 7, 6} karena tidak mengubah urutan pada array asli.
Misalkan subsekuens yang dipilih adalah S. S disebut valid apabila dari 1 <= i < |S| (|S| adalah panjang dari array S), banyaknya i dimana Si != Si + 1 tidak lebih dari 1. Sebagai contoh subsekuens {1, 3, 3} valid karena dua angka berurutan yang nilainya beda tidak lebih dari satu, sedangkan subsekuens {1, 6, 7} tidak valid karena jumlah dua angka berurutan yang nilainya beda ada dua. Bantu Pak Dengklek menentukan panjang S valid yang terpanjang!
Batasan:
1 <= N <= 100.000
Format Masukan:
Baris pertama berisi sebuah bilangan N.
Baris kedua berisi N bilangan, masing-masing menandakan elemen ke-i dari array pak Dengklek.
Format Keluaran:
Sebuah bilangan seperti deskripsi diatas.
Contoh Masukan dan Keluaran:
| Contoh Masukan | Contoh Keluaran |
|
4 1 1 1 1 |
4 |
|
6 1 1 2 1 2 2 |
5 |
|
7 1 2 2 4 3 5 2 |
3 |